题目内容
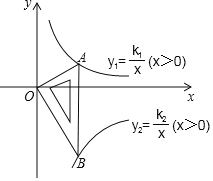
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与y轴交于点A,
的图象与y轴交于点A,
与x轴交于点B,与反比例函数![]() 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
标为2,
(1)求一次函数和反比例函数的解析式;
(2)直接写出![]() 时x的取值范围.
时x的取值范围.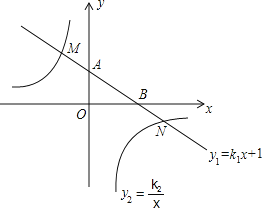
【答案】(1)y1=![]() x+1,
x+1,![]() (2)x<-2或0<x<4
(2)x<-2或0<x<4
【解析】
解:(1)∵一次函数![]() 的图象与y轴交于点A,与x轴交于点B,
的图象与y轴交于点A,与x轴交于点B,
∴A(0,1),B(![]() ,0).
,0).
∵△AOB的面积为1,∴![]() ×OB×OA=1,即
×OB×OA=1,即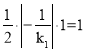 .∴
.∴![]() .
.
∴一次函数的解析式为y1=![]() x+1.
x+1.
∵点M在直线y1上,∴当y=2时,![]() x+1=2,解得x=-2.∴M的坐标为(-2,2)
x+1=2,解得x=-2.∴M的坐标为(-2,2)
又∵点M在反比例函数的图象上,∴k2=-2×2=-4,
∴反比例函数的解析式为![]() .
.
(2)当y1>y2时,x<-2或0<x<4.
(1)先由一次函数的解析式求出点A与点B的坐标,再根据△AOB的面积为1,可得到k1的值,
从而求出一次函数的解析式;得到点M的坐标,然后运用待定系数法即可求出反比例函数的解析式.
(2)y1>y2即一次函数值大于反比例函数值,只需观察一次函数的图象落在反比例函数的图象的
上方时自变量的取值范围即可,为此,先求出它们的交点坐标,再根据函数图象,可知在在点M的左边以及原点和点N之间的区间,y1>y2:
解方程组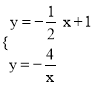 得
得![]() 或
或![]() ,
,
∴当y1>y2时,x<-2或0<x<4.

练习册系列答案
相关题目