题目内容
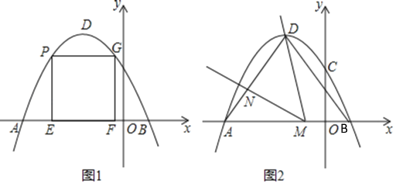
【题目】如图1,在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c经过点A(﹣5,0)和点B(1,0).
x2+bx+c经过点A(﹣5,0)和点B(1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)点P是抛物线上A、D之间的一点,过点P作PE⊥x轴于点E,PG⊥y轴,交抛物线于点G,过点G作GF⊥x轴于点F,当矩形PEFG的周长最大时,求点P的横坐标;
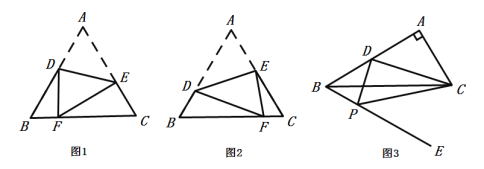
(3)如图2,连接AD、BD,点M在线段AB上(不与A、B重合),作∠DMN=∠DBA,MN交线段AD于点N,是否存在这样点M,使得△DMN为等腰三角形?若存在,求出AN的长;若不存在,请说明理由.
【答案】(1)抛物线的表达式为:y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() ,D(﹣2,4);(2)点P的横坐标为﹣
,D(﹣2,4);(2)点P的横坐标为﹣![]() ;(3)AN=1或
;(3)AN=1或![]() .
.
【解析】
(1)根据抛物线过A、B两点,可用交点式求出抛物线的解析式,然后求抛物线的顶点坐标即可;
(2)设点P(m,﹣![]() m2﹣
m2﹣![]() m+
m+![]() ),分别用m表示出PE和PG,从而得出矩形的周长与m的二次函数关系式,利用二次函数的顶点式求最值即可;
),分别用m表示出PE和PG,从而得出矩形的周长与m的二次函数关系式,利用二次函数的顶点式求最值即可;
(3)利用相似三角形的判定定理可得△BDM∽△AMN,列出比例式,并根据平面直角坐标系中任意两点之间的距离公式分别求出AB、AD、BD,最后根据等腰三角形的腰的情况分类讨论即可.
解:(1)∵抛物线y=﹣![]() x2+bx+c经过点A(﹣5,0)和点B(1,0)
x2+bx+c经过点A(﹣5,0)和点B(1,0)
∴抛物线的表达式为:y=﹣![]() (x+5)(x﹣1)=﹣
(x+5)(x﹣1)=﹣![]() x2﹣
x2﹣![]() x+
x+![]() ,
,
则顶点坐标的横坐标为:  ,代入可得顶点坐标的纵坐标为:4
,代入可得顶点坐标的纵坐标为:4
∴点D(﹣2,4);
(2)设点P(m,﹣![]() m2﹣
m2﹣![]() m+
m+![]() ),
),
则PE=﹣![]() m2﹣
m2﹣![]() m+
m+![]() ,PG=2(﹣2﹣m)=﹣4﹣2m,
,PG=2(﹣2﹣m)=﹣4﹣2m,
∴矩形PEFG的周长=2(PE+PG)=2(﹣![]() m2﹣
m2﹣![]() m+
m+![]() ﹣4﹣2m)=﹣
﹣4﹣2m)=﹣![]() (m+
(m+![]() )2+
)2+![]() ,
,
∵﹣![]() <0,故当m=﹣
<0,故当m=﹣![]() 时,矩形PEFG周长最大,
时,矩形PEFG周长最大,
此时,点P的横坐标为﹣![]() ;
;
(3)∵∠DMN=∠DBA,
∠BMD+∠BDM=180°﹣∠ADB,
∠NMA+∠DMB=180°﹣∠DMN,
∴∠NMA=∠MDB,
∴△BDM∽△AMN,
∴![]() ,
,
而AB=1-(﹣5)=6,AD=BD=![]() =5,
=5,
①当MN=DM时,
∴△BDM≌△AMN,
即:AM=BD=5,则AN=MB=AB-AM=1;
②当NM=DN时,
则∠NDM=∠NMD,
∴△AMD∽△ADB,
∴AD2=AB×AM,即:25=6×AM,则AM=![]() ,
,
而![]() ,即
,即 ,
,
解得:AN=![]() ;
;
③当DN=DM时,
∵∠DNM>∠DAB,而∠DAB=∠DMN,
∴∠DNM>∠DMN,
∴DN≠DM;
综上所述:AN=1或![]() .
.

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案【题目】探究函数y=x+![]() (x>0)与y=x+
(x>0)与y=x+![]() (x>0,a>0)的相关性质.
(x>0,a>0)的相关性质.
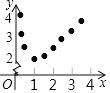
(1)小聪同学对函数y=x+![]() (x>0)进行了如下列表、描点,请你帮他完成连线的步骤;观察图象可得它的最小值为 ,它的另一条性质为 ;
(x>0)进行了如下列表、描点,请你帮他完成连线的步骤;观察图象可得它的最小值为 ,它的另一条性质为 ;
x | … |
|
|
| 1 |
| 2 |
| 3 | … |
y | … |
|
|
| 2 |
|
|
|
| … |
(2)请用配方法求函数y=x+![]() (x>0)的最小值;
(x>0)的最小值;
(3)猜想函数y=x+![]() (x>0,a>0)的最小值为 .
(x>0,a>0)的最小值为 .