题目内容
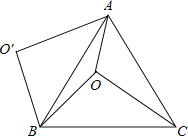
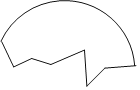
【题目】考古学家发现了一块古代圆形陶器残片如图所示，为了修复这块陶器残片，需要找出圆心．
（1）请利用尺规作图确定这块残片的圆心O；（保留作图痕迹，不写作法）
（2）写出作图的主要依据：_______________________________________________．
【答案】线段垂直平分线上的点与线段两个端点的距离相等；不在同一直线上的三个点确定一个圆．
【解析】试题分析：（1）直接在圆形残片上确定3点，进而作出两条垂直平分线的交点得出圆心即可；
（2）利用垂直平分线的性质得出圆心的位置．
试题解析：解：（1）如图所示，点O即为所求作的圆心；
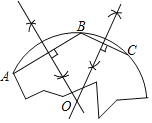
（2）作图的主要依据：
线段垂直平分线上的点与线段两个端点的距离相等；不在同一直线上的三个点确定一个圆．
练习册系列答案
相关题目
