题目内容
【题目】在平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△AEF,点O、B的对应点分别是点E、F.
(1)若点B的坐标是(﹣4,0),请在图中画出△AEF,并写出点E、F的坐标.
(2)当点F落在x轴的上方时,试写出一个符合条件的点B的坐标.
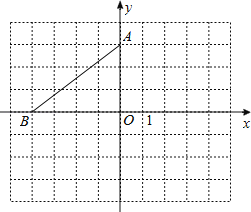
【答案】(1)见解析;点E的坐标是(3,3),点F的坐标是(3,﹣1).(2)B的坐标是(﹣2,0).
【解析】
试题分析:(1)△AOB绕点A逆时针旋转90°后得到△AEF,所以AO⊥AE,AB⊥AF,BO⊥EF,AO=AE,AB=AF,BO=EF,据此在图中画出△AEF,并写出点E、F的坐标即可.
(2)根据点F落在x轴的上方,可得EF<AO;然后根据EF=OB,判断出OB<3,即可求出一个符合条件的点B的坐标是多少.
解:(1)∵△AOB绕点A逆时针旋转90°后得到△AEF,
∴AO⊥AE,AB⊥AF,BO⊥EF,AO=AE,AB=AF,BO=EF,
∴△AEF在图中表示为:
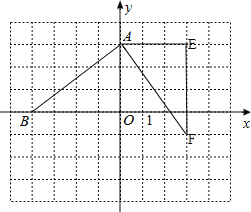
∵AO⊥AE,AO=AE,
∴点E的坐标是(3,3),
∵EF=OB=4,
∴点F的坐标是(3,﹣1).
(2)∵点F落在x轴的上方,
∴EF<AO,
又∵EF=OB,
∴OB<AO,AO=3,
∴OB<3,
∴一个符合条件的点B的坐标是(﹣2,0).

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目