题目内容
【题目】如图,在△ABC中AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是( )
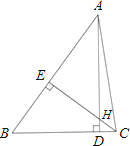
A.1 B.2 C.3 D.4
【答案】A
【解析】
试题分析:本题可先根据AAS判定△AEH≌△CEB,可得出AE=CE,从而得出CH=CE﹣EH=4﹣3=1.
解:在△ABC中,AD⊥BC,CE⊥AB,
∴∠AEH=∠ADB=90°;
∵∠EAH+∠AHE=90°,∠DHC+∠BCH=90°,
∵∠EHA=∠DHC(对顶角相等),
∴∠EAH=∠DCH(等量代换);
∵在△BCE和△HAE中
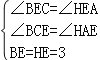 ,
,
∴△AEH≌△CEB(AAS);
∴AE=CE;
∵EH=EB=3,AE=4,
∴CH=CE﹣EH=AE﹣EH=4﹣3=1.
故选A.

练习册系列答案
相关题目