题目内容
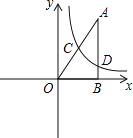
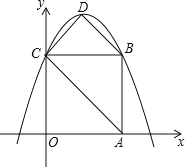
【题目】如图，在平面直角坐标系中，正方形OABC的边长为4，顶点A、C分别在x轴、y轴的正半轴，抛物线y=﹣
x2+bx+c经过B、C两点，点D为抛物线的顶点，连接AC、BD、CD．
（1）求此抛物线的解析式．
（2）求此抛物线顶点D的坐标和四边形ABCD的面积．
【答案】（1）y=﹣
x2+2x+4；（2）12．
【解析】
试题分析：（1）根据题意确定出B与C的坐标，代入抛物线解析式求出b与c的值，即可确定出解析式；
（2）把抛物线解析式化为顶点形式，找出顶点坐标，四边形ABDC面积=三角形ABC面积+三角形BCD面积，求出即可．
解：（1）由已知得：C（0，4），B（4，4），
把B与C坐标代入y=﹣
x2+bx+c得：
，
解得：b=2，c=4，
则解析式为y=﹣x2+2x+4；
（2）∵y=﹣x2+2x+4=﹣（x﹣2）2+6，
∴抛物线顶点坐标为（2，6），
则S四边形ABDC=S△ABC+S△BCD=×4×4+×4×2=8+4=12．
练习册系列答案
相关题目
