题目内容
【题目】如图,直线AC∥BD,连接AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA,PB,构成∠PAC,∠APB,∠PBD三个角.(提示:有公共端点的两条重合的射线所组成的角是0°角)
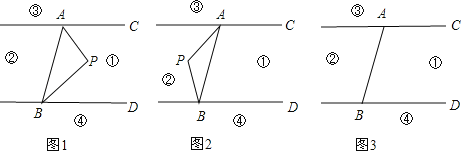
(1)当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?(直接回答成立或不成立)
(3)当动点P落在第③部分时,全面探究∠PAC,∠APB,∠PBD之间的关系,并写出动点P的具体位置和相应的结论.选择其中一种结论加以证明.
【答案】(1)证明解解析(2)不成立(3)(a)当动点P在射线BA的右侧时,结论是:∠PBD=∠PAC+∠APB.(b)当动点P在射线BA上,结论是:∠PBD=∠PAC+∠APB.或∠PAC=∠PBD+∠APB或∠APB=0°,∠PAC=∠PBD(任写一个即可).(c)当动点P在射线BA的左侧时,结论是∠PAC=∠APB+∠PBD.选择(a)证明见解析
【解析】
试题分析:(1)如图1,延长BP交直线AC于点E,由AC∥BD,可知∠PEA=∠PBD.由∠APB=∠PAE+∠PEA,可知∠APB=∠PAC+∠PBD;
(2)过点P作AC的平行线,根据平行线的性质解答;
(3)根据P的不同位置,分三种情况讨论.
解:(1)解法一:如图1延长BP交直线AC于点E.
∵AC∥BD,∴∠PEA=∠PBD.
∵∠APB=∠PAE+∠PEA,
∴∠APB=∠PAC+∠PBD;
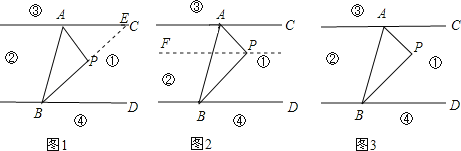
解法二:如图2
过点P作FP∥AC,
∴∠PAC=∠APF.
∵AC∥BD,∴FP∥BD.
∴∠FPB=∠PBD.
∴∠APB=∠APF+∠FPB
=∠PAC+∠PBD;
解法三:如图3,
∵AC∥BD,
∴∠CAB+∠ABD=180°,
∠PAC+∠PAB+∠PBA+∠PBD=180°.
又∠APB+∠PBA+∠PAB=180°,
∴∠APB=∠PAC+∠PBD.
(2)不成立.
(3)(a)当动点P在射线BA的右侧时,结论是:
∠PBD=∠PAC+∠APB.
(b)当动点P在射线BA上,结论是:
∠PBD=∠PAC+∠APB.
或∠PAC=∠PBD+∠APB或∠APB=0°,
∠PAC=∠PBD(任写一个即可).
(c)当动点P在射线BA的左侧时,
结论是∠PAC=∠APB+∠PBD.
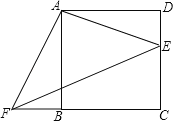
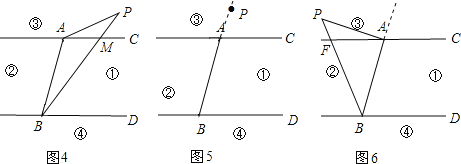
选择(a)证明:
如图4,连接PA,连接PB交AC于M.
∵AC∥BD,
∴∠PMC=∠PBD.
又∵∠PMC=∠PAM+∠APM(三角形的一个外角等于与它不相邻的两个内角的和),
∴∠PBD=∠PAC+∠APB.
选择(b)证明:如图5
∵点P在射线BA上,∴∠APB=0度.
∵AC∥BD,∴∠PBD=∠PAC.
∴∠PBD=∠PAC+∠APB
或∠PAC=∠PBD+∠APB
或∠APB=0°,∠PAC=∠PBD.
选择(c)证明:
如图6,连接PA,连接PB交AC于F
∵AC∥BD,∴∠PFA=∠PBD.
∵∠PAC=∠APF+∠PFA,
∴∠PAC=∠APB+∠PBD.

 期末集结号系列答案
期末集结号系列答案