题目内容
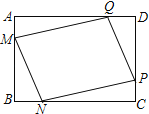
【题目】某小区在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化,为了绿化环境又节省成本.如图,已知矩形的边BC=200m,边AB=a m(a为不大于200的常数),四边形MNPQ的顶点在矩形的边上,且AM=BN=CP=DQ=x m,设四边形MNPQ的面积为S m2
(1)求S关于x的函数关系式,并直接写出自变量x的取值范围;
(2)若a=120,求S的最小值,并求出此时x的值;
(3)若a=200,且每平方米绿化费用需50元,则此时绿化最低费用为______万元.
【答案】(1)S=2x2-(a+200)x+200a,自变量x的取值范围是0<x<a;(2)a=120,S的最小值是11200,此时x的值是80;(3)100.
【解析】
(1)根据四边形MNPQ的面积等于矩形ABCD的面积减去四个直角三角形的面积即可求得S关于x的函数关系式,根据题意直接确定x的取值范围即可;(2)把a=120代入解析式,再利用二次函数求最值得方法解答即可;(3)把a=200代入解析式,再利用二次函数求最值得方法求得S的最小值,再计算最低费用即可.
解:(1)由题意可得,
S=200a-![]() =2x2-(a+200)x+200a(0<x<a)
=2x2-(a+200)x+200a(0<x<a)
即S关于x的函数关系式是S=2x2-(a+200)x+200a,自变量x的取值范围是0<x<a.
(2)当a=120时,
S=2x2﹣320x+200×120=2(x﹣80)2+11200,
∴x=80时,S取得最小值,此时,S=11200,
即a=120,S的最小值是11200,此时x的值是80;
(3)当a=200时,
S=2x2﹣(200+200)x+200×200=2(x﹣100)2+20000,
∴当x=100时,S取得最小值,此时S=20000,
20000×50=1000000(元)=100(万元),
即此时绿化最低费用为100万元,
故答案为:100.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】为了解学生每天的睡眠情况,某初中学校从全校 800 名学生中随机抽取了 40 名学生,调查了他们平均每天的睡眠时间(单位: h) ,统计结果如下:
9,8,10.5,7,9,8,10,9.5,8,9,9.5,7.5,9.5,9,8.5,7.5,10,9.5,8,9,
7,9.5,8.5,9,7,9,9,7.5,8.5,8.5,9,8,7.5,9.5,10,9.5,8.5,9,8,9.
在对这些数据整理后,绘制了如下的统计图表:
睡眠时间分组统计表 睡眠时间分布情况
组别 | 睡眠时间分组 | 人数(频数) |
1 | 7≤t<8 | m |
2 | 8≤t<9 | 11 |
3 | 9≤t<10 | n |
4 | 10≤t<11 | 4 |

请根据以上信息,解答下列问题:
(1) m = , n = , a = , b = ;
(2)抽取的这 40 名学生平均每天睡眠时间的中位数落在 组(填组别) ;
(3)如果按照学校要求,学生平均每天的睡眠时间应不少于 9 h,请估计该校学生中睡眠时间符合要求的人数.