Question

【题目】已知抛物线：(为常数)的顶点为．

(1)求点的坐标；(用含的式子表示)

(2)在同一平面直角坐标系中，存在函数图象，点在图象上，点在抛物线上，对于任意的实数，都有点，关于点对称．

①当时，求图象对应函数的解析式；

②当时，都有成立，结合图象，求的取值范围．

Answer 1

【答案】（1）顶点的坐标为；（2）①，②所求的取值范围为或．

【解析】

（1）把二次函数化为顶点式，即可得到答案；

（2）①根据题意，由轴对称的性质，有，然后整理得到，即可得到答案；

②根据题意，由两个函数图形的性质，可分成3种情况进行分析，画出图像，分别求出t的取值范围即可．

（1）

∴顶点的坐标为；

（2）①当时，得的解析式为：，

点在上，∴

∵点与点关于点对称，则点，到点的距离相等，此三点横坐标相同，有.

∴

整理，得，

由于为任意实数，令为自变量，为.

即可得的解析式为：；

②关于抛物线的性质：

点在上，∴

由：，知

抛物线开口向上，对称轴为，顶点，且图象恒过点.

∴当时，图象的随着的增大而增大.

当时，取最大值；当时，取最小值；

最大值比最小值大1.

关于图象的性质：

∵点与点关于点对称，

有，

，

整理，得

所以，图象的解析式为：.

配方，得

∴图象为一抛物线，开口向下，对称轴为，顶点，且图象恒过点.

∴当时，图象的随着的增大而增大.

当时，取最大值；当时，取最小值，即过；最大值比最小值大1.

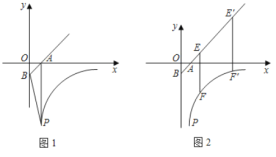
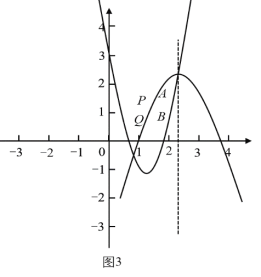
情况1：当，两点重合，即两个函数恰好都经过，时，把代入得，解得，或.

分别对应图3，图4两种情形，由图可知，当，或时，与重合，即有，不合题意，舍去；

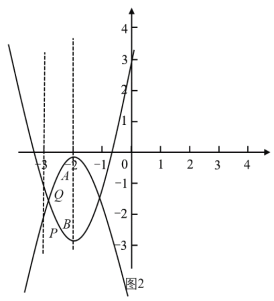
情况2：当点在点下方，即时，大致图象如图1，当时，大致图象如图2，都有点在点的上方，即成立，符合题意；

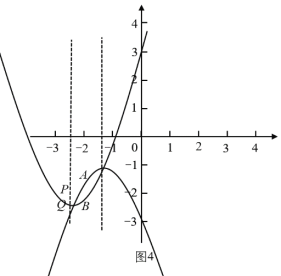
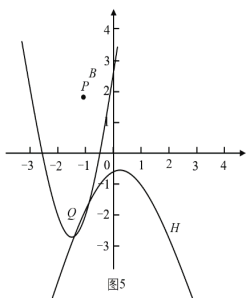
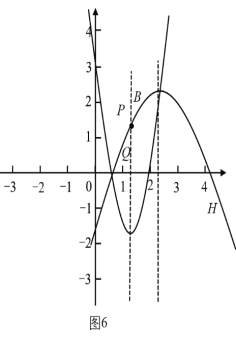
情况3：当点在点上方，即时，大致图象如图5，图6，当时，存在在的下方，即存在，不符合题意，舍去；

综上所述，所求的取值范围为：或.