题目内容
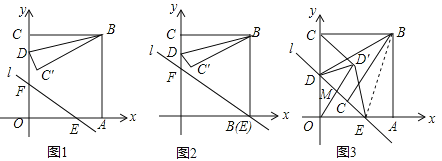
【题目】如图所示,沿AE折叠长方形ABCD使点D恰好落在BC边上的点F处.已知AB=8cm,BC=10cm. 
(1)求EC的长;
(2)求DE的长;
(3)求△AFE的面积.
【答案】
(1)解:∵AB=8cm,BC=10cm,
∴DC=8cm,AD=10cm,
又∵将△ADE折叠使点D恰好落在BC边上的点F,
∴AF=AD=10cm,DE=EF,
在Rt△ABF中,AB=8cm,AF=10cm,
∴BF= ![]() =6cm,
=6cm,
∴FC=10﹣6=4cm,
设DE=xcm,则EF=xcm,EC=(8﹣x)cm,
在Rt△CEF中,EF2=FC2+EC2,即x2=42+(8﹣x)2,解得x=5,
即DE的长为5cm,
EC=8﹣x=8﹣5=3,
即EC的长为3cm.
(2)解:∵AB=8cm,BC=10cm,
∴DC=8cm,AD=10cm,
又∵将△ADE折叠使点D恰好落在BC边上的点F,
∴AF=AD=10cm,DE=EF,
在Rt△ABF中,AB=8cm,AF=10cm,
∴BF= ![]() =6cm,
=6cm,
∴FC=10﹣6=4cm,
设DE=xcm,则EF=xcm,EC=(8﹣x)cm,
在Rt△CEF中,EF2=FC2+EC2,即x2=42+(8﹣x)2,解得x=5,
即DE的长为5cm,
(3)解:S△AEF= ![]() EF×AF=
EF×AF= ![]() ×10×5=25(cm2).
×10×5=25(cm2).
故△AFE的面积是25cm2.
【解析】(1)(2)根据矩形的性质得DC=8cm,AD=10cm,再根据折叠的性质得到AF=AD=10cm,DE=EF,在Rt△ABF中,利用勾股定理易得BF=6cm,设DE=xcm,则EF=xcm,EC=(8﹣x)cm,在Rt△CEF中,利用勾股定理可求出x的值,进一步得到EC的长,DE的长;(3)根据三角形面积公式计算即可求解.
【考点精析】关于本题考查的矩形的性质和翻折变换(折叠问题),需要了解矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能得出正确答案.

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案【题目】下表是篮球运动员在一些篮球比赛中罚球的记录:
罚球数 | 4 | 5 | 6 | 3 | 3 | 5 |
罚中球数 | 3 | 4 | 5 | 2 | 3 | 3 |
(1)计算表中“罚中频率不低于0.8”的有几次;
(2)根据这些罚球频率,估计该运动员的罚中球概率(精确0.01)
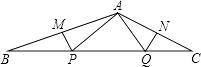
【题目】观察图形,解答问题:
(1)按下表已填写的形式填写表中的空格:
图① | 图② | 图③ | |
三个角上三个数的积 | 1×(﹣1)×2=﹣2 | (﹣3)×(﹣4)×(﹣5)=﹣60 | |
三个角上三个数的和 | 1+(﹣1)+2=2 | (﹣3)+(﹣4)+(﹣5)=﹣12 | |
积与和的商 | ﹣2÷2=﹣1 |
(2)请用你发现的规律求出图④中的数y和图⑤中的数x.