题目内容
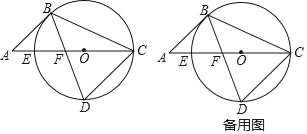
【题目】如图,在![]() 中,
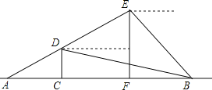
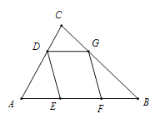
中,![]() ,AB=5,BC=4,点D为边AC上的动点,作菱形DEFG,使点E、F在边AB上,点G在边BC上.若这样的菱形能作出两个,则AD的取值范围是( )
,AB=5,BC=4,点D为边AC上的动点,作菱形DEFG,使点E、F在边AB上,点G在边BC上.若这样的菱形能作出两个,则AD的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】B
【解析】
因为在![]() 中只能作出一个正方形,所以要作两个菱形则AD必须小于此时的AD,也即这是AD的最大临界值;当AD等于菱形边长时,这时恰好可以作两个菱形,这是AD最小临界值.然后分别在这2种情形下,利用相似三角形的性质求出AD即可.
中只能作出一个正方形,所以要作两个菱形则AD必须小于此时的AD,也即这是AD的最大临界值;当AD等于菱形边长时,这时恰好可以作两个菱形,这是AD最小临界值.然后分别在这2种情形下,利用相似三角形的性质求出AD即可.
过C作![]() 交DG于M
交DG于M
由三角形的面积公式得![]()
即![]() ,解得
,解得![]()
①当菱形DEFG为正方形时,则只能作出一个菱形
设:![]() ,
,![]()
![]() 为菱形,
为菱形,![]()
![]() ,
,![]() ,即
,即 ,得
,得![]()
![]() (
(![]() )
)
若要作两个菱形,则![]() ;
;

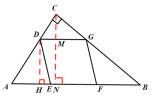
②当![]() 时,则恰好作出两个菱形
时,则恰好作出两个菱形
设:![]() ,
,![]()
过D作![]() 于H,
于H,![]()
![]()
由①知,![]() ,
, ,得
,得![]()
![]()
综上,![]()
故选:B.

练习册系列答案
相关题目
【题目】已知:二次函数![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请直接写出m的值为_________.
(2)求出这个二次函数的解析式.
(3)当![]() 时,则y的取值范围为______________________________.
时,则y的取值范围为______________________________.