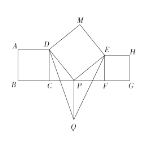
题目内容
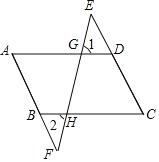
【题目】如图,![]() 为正方形
为正方形![]() 的边
的边![]() 的延长线上一动点,以
的延长线上一动点,以![]() 为一边做正方形
为一边做正方形![]() ,以
,以![]() 为一顶点作正方形
为一顶点作正方形![]() ,且
,且![]() 在
在![]() 的延长线上(提示:正方形四条边相等,且四个内角为
的延长线上(提示:正方形四条边相等,且四个内角为![]() )
)
(1)若正方形![]() 、
、![]() 的面积分别为
的面积分别为![]() ,
,![]() ,则正方形
,则正方形![]() 的面积为 (直接写结果).
的面积为 (直接写结果).
(2)过点![]() 做
做![]() 的垂线交
的垂线交![]() 的平分线于点
的平分线于点![]() ,连接
,连接![]() ,试探求在点
,试探求在点![]() 运动过程中,
运动过程中,![]() 的大小是否发生变化,并说明理由.
的大小是否发生变化,并说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 的大小不会发生变化,理由见解析.
的大小不会发生变化,理由见解析.
【解析】
(1)先通过全等,得到EF=CP,通过勾股定理求![]() =
=![]() ,则正方形
,则正方形![]() 的面积=
的面积=![]() =
=![]() =
=![]()
(2)先通过证明![]() ,再通过正方形的性质得到
,再通过正方形的性质得到![]() ,再通过证明得到
,再通过证明得到![]() =45°,所以
=45°,所以![]() 的大小不会发生变化.
的大小不会发生变化.
(1) ∵四边形ABCD、四边形EFGH、四边形DPEM是正方形
∴DP=PE,∠DPE=90°,∠BCD=90°,∠EFG=90°
∴∠PCD=∠EFP=90°,∠DPC+∠PDC=90°, ∠EPF+∠DPC=90°,
∴∠PDC= ∠EPF
∴△CDP≌△FEP
∴EF=CP
∵在Rt△CDP中,![]() ,正方形
,正方形![]() 的面积=
的面积=![]() =a,正方形
=a,正方形![]() 的面积=
的面积=![]() =
=![]()
∴正方形![]() 的面积=
的面积=![]() =
=![]() =
=![]()
(2)![]() 的大小不会发生变化,理由如下,
的大小不会发生变化,理由如下,
![]()
![]()
![]()
![]() 平分
平分![]()
![]()
![]()
在正方形![]() 中,
中,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 的大小不会发生变化.
的大小不会发生变化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目