题目内容
如图:已知D为等腰直角△ABC斜边BC上的一个动点(D与B、C均不重合),连结AD,△ADE是等腰直角三角形,DE为斜边,连结CE.
①判断∠ECD的度数并说明理由.
②当△ABC、△ADE都是等边三角形,D点为△ABC中BC边上的一个动点(D与B、C均不重合),当点D运动到什么位置时,△DCE的周长最小?请探求点D的位置,并说明理由及求出此时∠EDC的度数.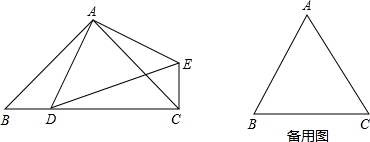
①判断∠ECD的度数并说明理由.
②当△ABC、△ADE都是等边三角形,D点为△ABC中BC边上的一个动点(D与B、C均不重合),当点D运动到什么位置时,△DCE的周长最小?请探求点D的位置,并说明理由及求出此时∠EDC的度数.

分析:(1)首先根据等腰直角三角形的性质得出∠BAD=∠CAE,即可得出△ABD≌△ACE(SAS),进而得出答案即可;
(2)理由等边三角形性质结合(1)的做法得出△ABD≌△ACE,进而得出当△DCE的周长最小即DE最短即可,结合等边三角形的性质得出即可.
(2)理由等边三角形性质结合(1)的做法得出△ABD≌△ACE,进而得出当△DCE的周长最小即DE最短即可,结合等边三角形的性质得出即可.
解答:解:(1)∠ECD=90°,
理由:∵如图1所示:
△ABC,△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,∠DAC+∠CAE=90°,∠ABC=∠ACB=45°,
∴∠BAD=∠CAE,
在△ABD和△ACE中
,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE=45°,
∴∠ECD=45°+45°=90°.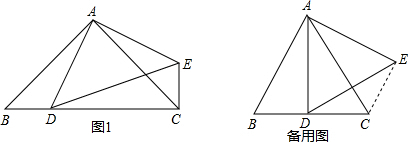
(2)点D运动到BC的中点时,△DCE的周长最小;
理由:如备用图所示:
∵△ABC,△ADE都是等边三角形,
∴AB=AC=BC,AD=AE=DE,∠BAC=∠DAE=60°,∠BAD+∠DAC=60°,∠DAC+∠CAE=60°,
∴∠BAD=∠CAE,
在△ABD和△ACE中
,
∴△ABD≌△ACE(SAS),
∴EC=BD,
∴DC+EC=BC,即DC+EC是固定长度,
当△DCE的周长最小即DE最短即可,
∵当AD⊥BC时,AD最短则DE最短,
∵△ABC是等边三角形,
∴当AD⊥BC,则BD=CD,即D为BC的中点时,△DCE的周长最小,
∵BD=DC,BD=CE,
∴CD=EC,
∵∠ABC=∠ACE=∠ACD=60°,
∴∠DCE=120°,
∴∠EDC=∠CED=30°.
理由:∵如图1所示:
△ABC,△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,∠DAC+∠CAE=90°,∠ABC=∠ACB=45°,
∴∠BAD=∠CAE,
在△ABD和△ACE中
|
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE=45°,
∴∠ECD=45°+45°=90°.

(2)点D运动到BC的中点时,△DCE的周长最小;
理由:如备用图所示:
∵△ABC,△ADE都是等边三角形,
∴AB=AC=BC,AD=AE=DE,∠BAC=∠DAE=60°,∠BAD+∠DAC=60°,∠DAC+∠CAE=60°,
∴∠BAD=∠CAE,
在△ABD和△ACE中
|
∴△ABD≌△ACE(SAS),
∴EC=BD,
∴DC+EC=BC,即DC+EC是固定长度,
当△DCE的周长最小即DE最短即可,
∵当AD⊥BC时,AD最短则DE最短,
∵△ABC是等边三角形,
∴当AD⊥BC,则BD=CD,即D为BC的中点时,△DCE的周长最小,
∵BD=DC,BD=CE,
∴CD=EC,
∵∠ABC=∠ACE=∠ACD=60°,
∴∠DCE=120°,
∴∠EDC=∠CED=30°.
点评:此题主要考查了等腰三角形以及等边三角形的性质和全等三角形的判定与性质等知识,根据已知得出△ABD≌△ACE是解题关键.

练习册系列答案
相关题目

 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A= 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.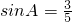 ,其中A为锐角,试求sadA的值;
,其中A为锐角,试求sadA的值; ,通常写成1:m的形式).
,通常写成1:m的形式).
 ,通常写成1:m的形式).
,通常写成1:m的形式).