ΧβΡΩΡΎ»ί
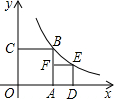
»γΆΦΘ§“―÷ΣΘΚ“Μ¥ΈΚ· ΐΘΚy=-x+4ΒΡΆΦœσ”κΖ¥±»άΐΚ· ΐΘΚy=
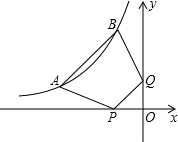
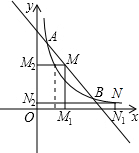
Θ®xΘΨ0Θ©ΒΡΆΦœσΖ÷±πΫΜ”ΎAΓΔBΝΫΒψΘ§ΒψM «“Μ¥ΈΚ· ΐΆΦœσ‘ΎΒΎ“Μœσœό≤ΩΖ÷…œΒΡ»Έ“β“ΜΒψΘ§ΙΐMΖ÷±πœρx÷αΓΔy÷αΉς¥ΙœΏΘ§¥ΙΉψΖ÷±πΈΣM1ΓΔM2Θ§…ηΨΊ–ΈMM1OM2ΒΡΟφΜΐΈΣS1ΘΜΒψNΈΣΖ¥±»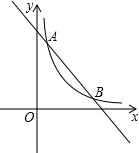 άΐΚ· ΐΆΦœσ…œ»Έ“β“ΜΒψΘ§ΙΐNΖ÷±πœρx÷αΓΔy÷αΉς¥ΙœΏΘ§¥ΙΉψΖ÷±πΈΣN1ΓΔN2Θ§…ηΨΊ–ΈNN1ON2ΒΡΟφΜΐΈΣS2ΘΜ
άΐΚ· ΐΆΦœσ…œ»Έ“β“ΜΒψΘ§ΙΐNΖ÷±πœρx÷αΓΔy÷αΉς¥ΙœΏΘ§¥ΙΉψΖ÷±πΈΣN1ΓΔN2Θ§…ηΨΊ–ΈNN1ON2ΒΡΟφΜΐΈΣS2ΘΜ
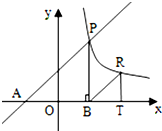
Θ®1Θ©»τ…ηΒψMΒΡΉχ±ξΈΣΘ®xΘ§yΘ©Θ§«κ–¥≥ωS1ΙΊ”ΎxΒΡΚ· ΐ±μ¥ο ΫΘ§≤Δ«σx»ΓΚΈ÷Β ±Θ§S1ΒΡΉν¥σ÷ΒΘΜ
Θ®2Θ©Ιέ≤λΆΦ–ΈΘ§Ά®Ιΐ»ΖΕ®xΒΡ»Γ÷ΒΘ§ ‘±»ΫœS1ΓΔS2ΒΡ¥σ–ΓΘ°
| 2 |
| x |
 άΐΚ· ΐΆΦœσ…œ»Έ“β“ΜΒψΘ§ΙΐNΖ÷±πœρx÷αΓΔy÷αΉς¥ΙœΏΘ§¥ΙΉψΖ÷±πΈΣN1ΓΔN2Θ§…ηΨΊ–ΈNN1ON2ΒΡΟφΜΐΈΣS2ΘΜ
άΐΚ· ΐΆΦœσ…œ»Έ“β“ΜΒψΘ§ΙΐNΖ÷±πœρx÷αΓΔy÷αΉς¥ΙœΏΘ§¥ΙΉψΖ÷±πΈΣN1ΓΔN2Θ§…ηΨΊ–ΈNN1ON2ΒΡΟφΜΐΈΣS2ΘΜΘ®1Θ©»τ…ηΒψMΒΡΉχ±ξΈΣΘ®xΘ§yΘ©Θ§«κ–¥≥ωS1ΙΊ”ΎxΒΡΚ· ΐ±μ¥ο ΫΘ§≤Δ«σx»ΓΚΈ÷Β ±Θ§S1ΒΡΉν¥σ÷ΒΘΜ
Θ®2Θ©Ιέ≤λΆΦ–ΈΘ§Ά®Ιΐ»ΖΕ®xΒΡ»Γ÷ΒΘ§ ‘±»ΫœS1ΓΔS2ΒΡ¥σ–ΓΘ°
Θ®1Θ©ΓΏMΒΡΉχ±ξΈΣΘ®xΘ§yΘ©Θ§MΒψ‘ΎΚ· ΐy=-x+4ΒΡΆΦœσ…œΘ§
Γύy=-x+4Θ§
ΓύS1=xy=xΘ®-x+4Θ©=-x2+4x=-Θ®x-2Θ©2+4Θ§
Β±x=2 ±Θ§S1Ήν¥σ÷Β=4ΘΜ
Θ®2Θ©…ηNΘ®x1Θ§y1Θ©Θ§ΒψN‘ΎΖ¥±»άΐΚ· ΐy=
ΆΦœσ…œΘ§
ΓύS2=x1ΓΝy1=2Θ§
”…S1=S2Ω…ΒΟΘΚ-x2+4x=2Θ§Φ¥x2-4x+2=0Θ§
Γύx=2Γά
Θ§
Ά®ΙΐΙέ≤λΆΦœσΩ…ΒΟΘΚ
Β±x=2Γά
±Θ§S1=S2Θ§
Β±0ΘΦxΘΦ2-
Μρ2+
ΘΦxΘΦ4 ±Θ§S1ΘΦS2Θ§
Β±2-
ΘΦxΘΦ2+
±Θ§S1ΘΨS2Θ°
Γύy=-x+4Θ§
ΓύS1=xy=xΘ®-x+4Θ©=-x2+4x=-Θ®x-2Θ©2+4Θ§
Β±x=2 ±Θ§S1Ήν¥σ÷Β=4ΘΜ
Θ®2Θ©…ηNΘ®x1Θ§y1Θ©Θ§ΒψN‘ΎΖ¥±»άΐΚ· ΐy=
| 2 |
| x |
ΓύS2=x1ΓΝy1=2Θ§
”…S1=S2Ω…ΒΟΘΚ-x2+4x=2Θ§Φ¥x2-4x+2=0Θ§
Γύx=2Γά
| 2 |
Ά®ΙΐΙέ≤λΆΦœσΩ…ΒΟΘΚ
Β±x=2Γά
| 2 |
Β±0ΘΦxΘΦ2-
| 2 |
| 2 |
Β±2-
| 2 |
| 2 |


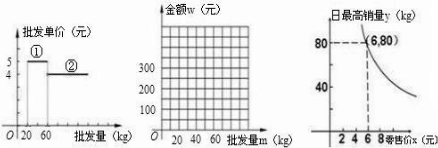
ΝΖœΑ≤αœΒΝ–¥πΑΗ
 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ