题目内容
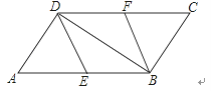
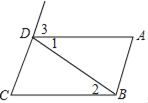
【题目】如图,填空并填写理由:
(1)因为∠1=∠2,所以AD∥BC__________.
(2)因为∠A+∠ABC=180°,所以AD∥BC________.
(3)因为_____∥________,所以∠C+∠ABC=180°(两直线平行,同旁内角互补)
(4)因为______∥______,所以∠3=∠C(两直线平行,同位角相等).
【答案】内错角相等,两直线平行;同旁内角互补,两直线平行;DC;AB;AD;BC.
【解析】
利用平行线的性质和判定解答即可.
(1)因为∠1=∠2,所以AD∥BC(内错角相等,两直线平行)
(2)因为∠A+∠ABC=180°,所以AD∥BC(同旁内角互补,两直线平行)
(3)因为DC∥AB,所以∠C+∠ABC=180°(两直线平行,同旁内角互补)
(4)因为AD∥BC,所以∠3=∠C(两直线平行,同位角相等)
故答案为:内错角相等,两直线平行;同旁内角互补,两直线平行;DC;AB;AD;BC.

练习册系列答案
相关题目
【题目】某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其他项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
运动项目 | 频数 | 频率 |
篮球 | 30 | 0.25 |
羽毛球 | m | 0.20 |
乒乓球 | 36 | n |
跳绳 | 18 | 0.15 |
其他 | 12 | 0.10 |
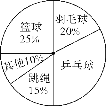
请根据以上图表信息,解答下列问题:
(1)频数分布表中的m=_________,n=_________;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为_________.