Question

【题目】从如图，在Rt△ABC中，∠C=90°，AC=3，BC=4，点F在边AC上，并且CF=1，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是（ ）

A. B. C. D.

Answer 1

【答案】A

【解析】延长FP交AB于M，当FP⊥AB时，点P到AB的距离最小，利用△AFM∽△ABC，得到，求出FM即可解决问题．

如图，延长FP交AB于M，当FP⊥AB时，点P到AB的距离最小．（点P在以F为圆心CF为半径的圆上，当FP⊥AB时，点P到AB的距离最小）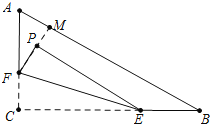

∵∠A=∠A，∠AMF=∠C=90°，
∴△AFM∽△ABC，
∴，
∵CF=1，AC=3，BC=4，
∴AF=2，AB=，
∴，
∴FM=，
∵PF=CF=1，
∴PM=
∴点P到边AB距离的最小值是．
故选：A．