Question

【题目】如图，O为坐标原点，四边形OABC为矩形，A（20，0），C（0，8），点D是OA的中点，点P在边BC上运动，当△ODP是以OD为腰的等腰三角形时，则P点的坐标为_____．

Answer 1

【答案】（6，8）或（4，8）或（16，8）

【解析】

若OD是等腰三角形的一条腰时，则有当点O是顶角顶点和当D是顶角顶点时两种情况，分别进行讨论得出P点的坐标即可．

（1）当若点O是顶角顶点时，P点就是以点O为圆心，以10为半径的弧与CB的交点，
在直角△OPC中，CP==6，
则P的坐标是（6，8）．
（2）当D是顶角顶点时，P点就是以点D为圆心，以10为半径的弧与CB的交点，
过D作DM⊥BC于点M，

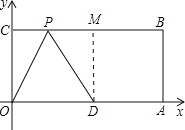
在直角△PDM中，PM==6，
当P在M的左边时，CP=10-6=4，则P的坐标是（4，8）；
当P在M的右侧时，CP=5+3=8，则P的坐标是（16，8）．
故P的坐标为：（6，8）或（4，8）或（16，8）．