题目内容
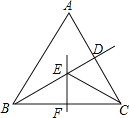
【题目】如图,△ABC是等腰直角三角形,延长BC至E使BE=BA,过点B作BD⊥AE于点D,BD与AC交于点F,连接EF.
(1)求证:BF=2AD;
(2)若CE=![]() ,求AC的长.
,求AC的长.

【答案】(1)见解析(2)2+
【解析】试题分析:(1)由△ABC是等腰直角三角形,得到AC=BC,∠FCB=∠ECA=90°,由于AC⊥BE,BD⊥AE,根据垂直的定义得到∠CBF+∠CFB=90°,∠DAF+∠AFD=90°,由于∠CFB=∠AFD,于是得到∠CBF=∠CAE,证得△BCF≌△ACE,得出AE=BF,由于BE=BA,BD⊥AE,于是得到AD=ED,即AE=2AD,即可得到结论;
(2)由(1)知△BCF≌△ACE,推出CF=CE=,在Rt△CEF中,EF=![]() =2,由于BD⊥AE,AD=ED,求得AF=FE=2,于是结论即可.
=2,由于BD⊥AE,AD=ED,求得AF=FE=2,于是结论即可.
(1)证明:∵△ABC是等腰直角三角形,
∴AC=BC,∴∠FCB=∠ECA=90°,
∵AC⊥BE,BD⊥AE,
∴∠CBF+∠CFB=90°,∠DAF+∠AFD=90°,
∵∠CFB=∠AFD,
∴∠CBF=∠CAE,
在△BCF与△ACE中,![]() ,
,
∴△BCF≌△ACE,
∴AE=BF,
∵BE=BA,BD⊥AE,
∴AD=ED,即AE=2AD,
∴BF=2AD;
(2)由(1)知△BCF≌△ACE,
∴CF=CE=,
∴在Rt△CEF中,EF=![]() =2,
=2,
∵BD⊥AE,AD=ED,
∴AF=FE=2,
∴AC=AF+CF=2+.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目