��Ŀ����
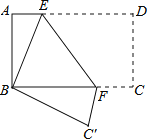
����Ŀ����ͼ�٣��ڳ�����ABCD�У�AB=10cm��BC=8cm����P��A��������A��B��C��D·���˶�����Dֹͣ����P���ٶ�Ϊÿ��1cm��a��ʱ��P���ٶȱ�Ϊÿ��bcm��ͼ���ǵ�P����x�����APD�����S1��cm2����x���룩�ĺ�����ϵͼ����
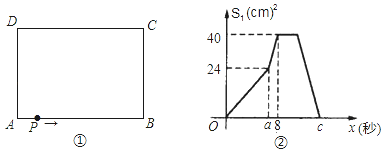
��1������ͼ�����ṩ����Ϣ����a��b��ͼ����c��ֵ��
��2�����P�뿪��A��·��Ϊy��cm������д������P�ı��ٶȺ�y���������˶�ʱ��x���룩�ĺ�����ϵʽ��
��3����P�������룬��APD�����S1�dz�����ABCD�����![]() ��
��
���𰸡�(1)a=6,b=2,c=17;(2) y=2x��6;(3) 5���14.5��.
��������
��1�����������ε������ʽ����a��b��ͼ����c��ֵ��
��2��ȷ��y��x�ĵ�����ϵ���г���ϵʽ���ɣ�
��3����P��AB���˶�ʱ��S��APD=![]() ��APΪ�˶�ʱ��t��һ�κ�����
��APΪ�˶�ʱ��t��һ�κ�����
��P��BC���˶�ʱS��APD=![]() Ϊ��ֵ��
Ϊ��ֵ��
��P��DC�����˶�ʱ��S��APD=![]() ��DPΪP���˶�ʱ���һ�κ�����
��DPΪP���˶�ʱ���һ�κ�����
�ȼ�����APD�������Ȼ�����������ֵ�����������IJ�ͬ�ֶΣ������Ӧ��x��ֵ���������xֵ�ڶ�Ӧ�ķֶ������ڣ���x��ֵ��Ϊ����Ľ⣬��֮���ǣ�
�⣺��1������ͼ���֪S��APD=![]() =
=![]() ��8����1��a��=24
��8����1��a��=24
��a=6
![]() =2
=2
![]() =17
=17
��2����a=6��b=2��
�ද��P�ı��ٶȺ�y���������˶�ʱ��x���룩�ĺ�����ϵʽΪ��y=6+2��x��6��=2x��6
��3���ٵ�0��x��6ʱ
AP=x��cm��
S��APD=![]() =4x
=4x
�ڵ�6��x��8ʱ
AP=6+��x��6����2=2x��6
S��APD=![]() =8x��24
=8x��24
�۵�x�˶���C��ʱ
2x��6=18��ã�x=12
����8��x��12ʱ
S��APD=![]() =40
=40
�ܵ�12��x��17ʱ
DP=2DC+BC����2x��6��=��2x+34
S��APD=![]() =��8x+136
=��8x+136
���ϣ�S��APD= ��
��
S��APD=![]() =20
=20
��4x=20ʱ��x=5��[0��6]������
��2x��6=20ʱ��x=13��6��8]����ȥ
��8��x��12ʱ��S��APD=40��24����ȥ
����8x+136=20��x=14.5����8��12]������
���Ե�P������5���14.5�룬��APD�����S1�dz�����ABCD�����![]() ��
��

����Ŀ��ij������˾��֯20������װ�˼ס��ҡ����������ز���120��ȥ����������ƻ�20������Ҫװ��,ÿ������ֻ��װ��ͬһ�����ز�,�ұ���װ��,�����±��ṩ����Ϣ,�����������
���ز����� | �� | �� | �� |
ÿ������������(��) | 8 | 6 | 5 |
ÿ�����ز�����(��Ԫ) | 12 | 16 | 10 |
(1)��װ�˼������ز��ij�����Ϊx,װ���������ز��ij�����Ϊy,��y��x֮��ĺ�����ϵʽ��
(2)���װ��ÿ�����ز��ij�����������3��,��ô�����İ��ŷ����м���?��д��ÿ�ְ��ŷ�����
(3)��Ҫʹ�˴����ۻ������,Ӧ����(2)�����ְ��ŷ���?�������������ֵ