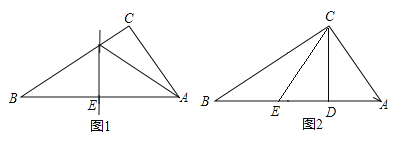
��Ŀ����
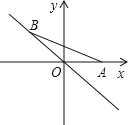
����Ŀ����ͼ����֪һ�κ���y=��![]() x+b��ͼ����A��2��3����AB��x�ᣬ����ΪB������OA��
x+b��ͼ����A��2��3����AB��x�ᣬ����ΪB������OA��
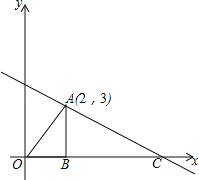
��1�����һ�κ����Ľ���ʽ�������һ�κ�����x��Ľ���C�����ꣻ
��2�����PΪֱ��y=��![]() x+b�ڵ�һ�����ڵ�ͼ���ϵ�һ���㣬����OBP�����S��x֮��ĺ�����ϵʽ����д���Ա���x�ķ�Χ��
x+b�ڵ�һ�����ڵ�ͼ���ϵ�һ���㣬����OBP�����S��x֮��ĺ�����ϵʽ����д���Ա���x�ķ�Χ��
��3�����MΪ��������һ�㣬��S��MAC=24��ֱ��д���������������ĵ�M�����꣮
���𰸡���1��һ�κ����Ľ���ʽΪy=��![]() ����C������Ϊ��8��0����
����C��������8��0����
��2��S=��![]() ��0��x��8����
��0��x��8����
��3����M������ΪM����8��0����M��24��0����M��0��12����M��0����4����
��������
�����������1������A���������һ�κ����Ľ���ʽ�ã���![]() ��2+b=3�����b=4�����һ�κ����Ľ���ʽΪy=��
��2+b=3�����b=4�����һ�κ����Ľ���ʽΪy=��![]() +4����y=0������x=8����C������Ϊ��8��0����
+4����y=0������x=8����C��������8��0����
��2������P��PD��OC������ΪD�����P������Ϊ��x����![]() ������DP=
������DP=![]() ���ɵ�A������Ϊ��2��3����֪��B������Ϊ��2��0�����ʴ�OB=2���������ε������ʽ��֪S=
���ɵ�A������Ϊ��2��3����֪��B������Ϊ��2��0�����ʴ�OB=2���������ε������ʽ��֪S=![]() ��
��
��3����Ϊ��M��x���Ϻ�y���������������ͼ�Σ�Ȼ���ٸ��������ε������ʽ�г����ڵ�M����ķ�����⼴�ɣ�
�⣺��1������x=2��y=3����ã���![]() ��2+b=3����ã�b=4��
��2+b=3����ã�b=4��
��һ�κ����Ľ���ʽΪy=��![]() ��
��
����y=0����ã�![]() =0�����x=8��
=0�����x=8��
����C��������8��0����
��2����ͼ1��ʾ������P��PD��OC������ΪD��
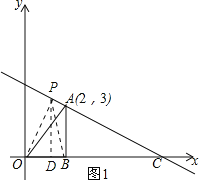
���P��������x����![]() ������DP=
������DP=![]() ��
��
��AB��OC��A��2��3����
����B��2��0����
��OB=2��
��![]() =
=![]() =��
=��![]() ��
��
��S=��![]() ��0��x��8����
��0��x��8����
��3����ͼ2��ʾ��

������M��x������λ�ڵ�C���ʱ�����M������Ϊ��a��0������MC=8��a��
��S��MAC=24��
��![]() ����
����![]() ��
��
��ã�a=��8��
����M����������8��0����
������Mλ�ڵ�M����ʱ�����M��������Ϊ��a��0������M��C=a��8��
��S��MAC=24��
��![]() ����
����![]() ��
��
��ã�a=24��
����M��������24��0����
��ͼ3��ʾ��
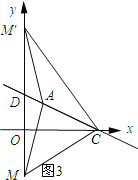
����x=0����y=��![]() �ã�y=4��
�ã�y=4��
����D��������0��4����
������Mλ�ڵ�D���·�ʱ�����M������Ϊ��0��a������DM=4��a��
��S��ACM=SMCD��S��MDA=24��
��![]() ��
��![]() =24��
=24��
��ã�a=��4��
����M��������0����4����
������Mλ�ڵ�M����ʱ�����M������Ϊ��0��a������DM=a��4��
��S��ACM=SMCD��S��MDA=24��
��![]() =24��
=24��
��ã�a=12��
����M��������0��12����
������������M������ΪM����8��0����M��24��0����M��0��12����M��0����4����