题目内容
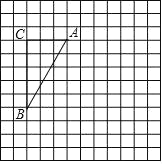
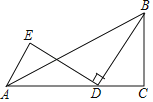
【题目】如图①,已知线段AB和直线l,用直尺和圆规在l上作出所有的点P,使得∠APB=30°,如图②,小明的作图方法如下:
第一步:分别以点A,B为圆心,AB长为半径作弧,两弧在AB上方交于点O;
第二步:连接OA,OB;
第三步:以O为圆心,OA长为半径作⊙O,交l于P1,P2;
所以图中P1,P2即为所求的点.
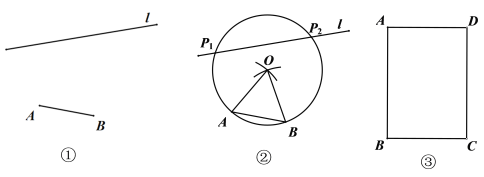
(1)在图②中,连接P1A,P1B,证明∠AP1B=30°;
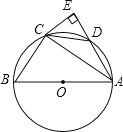
(2)如图③,用直尺和圆规在矩形ABCD内作出所有的点P,使得∠BPC=45°,(不写做法,保留作图痕迹).
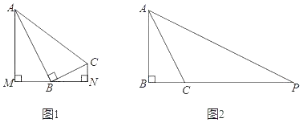
(3)已知矩形ABCD,若BC=2.AB=m,P为AD边上的点,若满足∠BPC=45°的点P恰有两个,则m的取值范围为______________.
【答案】(1)30°;(2)详见解析;(3)2≤m<![]()
【解析】
(1)由等边三角形得:∠AOB=60°,则根据圆周角定理可得:∠AP1B=30°;
(2)作等腰直角三角形BEC,BFC,再作△EBC的外接圆,可得圆心角∠BOC=90°,则BC所对的圆周角都是45°;
(3)先确定⊙O,根据同弧所对的圆周角相等,可得AD在四边形GEFH内部时符合条件,再进行求解即可;
答案:(1)∵OA=OB=AB,
∴△OAB是等边三角形,
∴∠AOB=60°,
由图②得:∠AP1B= ∠AOB=30°;
(2)如图③,①以B、C为圆心,以BC为半径作圆,交AB、DC于E、F,
②作BC的中垂线,连接EC,交于O,
③以O为圆心,OE为半径作圆,
则 上所有的点(不包括E、F两点)即为所求;
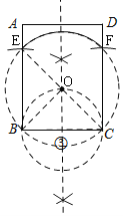
(3)如图:作⊙O
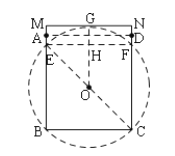
∵BE=BC=2
∴CE=![]()
∴⊙O的半径为![]() v2,即OE=0G=
v2,即OE=0G=![]() ,
,
∵OG⊥EF
∴EH=1,
∴Oн=1,
∴GH=![]() -1,
-1,
∴BE≤AB<MB,
∴2≤m<2+![]() -1,即2<m<
-1,即2<m<![]() +1,
+1,
故答案为:2≤m<![]()

【题目】已知二次函数![]() 的y与x的部分对应值如表:
的y与x的部分对应值如表:
x | 1 | 0 | 2 | 3 | 4 |
y | 5 | 0 | 4 | 3 | 0 |
下列结论:①抛物线的开口向上;②抛物线的对称轴为直线x=2;③当0<x<4时,y>0;④抛物线与x轴的两个交点间的距离是4;⑤若A(![]() ,2),B(
,2),B(![]() ,3)是抛物线上两点,则
,3)是抛物线上两点,则![]() ,其中正确的个数是 ( )
,其中正确的个数是 ( )
A. 2B. 3C. 4D. 5
【题目】抛物线![]() 上部分点的横坐标x纵坐标y的对应值如下表
上部分点的横坐标x纵坐标y的对应值如下表
x |
|
|
| 0 | 1 | 2 |
|
y |
| 0 |
|
| 0 | 8 |
|
![]() 写出该抛物线的对称轴及当
写出该抛物线的对称轴及当![]() 时对应的函数值;
时对应的函数值;
![]() 求出抛物线
求出抛物线![]() 的解析式,并在平面直角坐标系中画出该抛物线的图象;
的解析式,并在平面直角坐标系中画出该抛物线的图象;
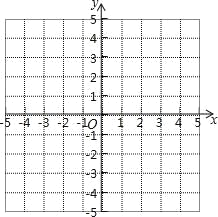
(3)结合图象回答:
①不等式![]() 的解集是___________________;
的解集是___________________;
②当![]() 时,y的取值范围是__________________.
时,y的取值范围是__________________.