Question

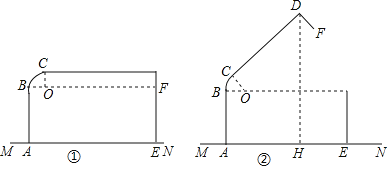
【题目】如图①是一个小箱子ABCDE放在桌面MN上的示意图，BC这部分可弯曲，在弯曲时形成一段圆弧，设圆弧所在圆的圆心为O，线段AB，CD均与圆弧相切，点B，C分别为切点，小箱子盖面CD与桌面MN平行，此时CD距离桌面14cm，已知AB的长10cm，CD的长为25.2cm．

（1）如图①，求弧BC的长度（结果保留π）．

（2）如图②，若小箱子ABCDE打开后弧BC所对的圆心角度数为60°，求小箱子顶端D到桌面MN的距离DH（结果保留一位小数）．（参考数据：≈1.73）

Answer 1

【答案】（1）2π（cm）；（2）顶端D到桌面MN的距离是27.8 cm

【解析】

（1）根据题意推出∠BOC＝90°，半径OC为4cm，即可得出弧BC的长度；

（2）过点C作CP⊥DH于点P，作CG⊥OB于G，得矩形CGQP，则CP∥OB，由题可得DP＝CD＝×25.2＝12.6cm，根据弧BC的长度为2πcm，可得OB＝OC＝6cm，由此可得CG＝OCsin60°＝6×＝3≈5.2cm，即可求出DH．

解：（1）如图①，

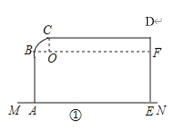
∵线段AB，CD均与圆弧相切，

∴OB⊥AB，OC⊥CD，

∴CD∥OB∥AM，

∴∠BOC＝∠OCD＝90°，

∵CD距离桌面14cm，AB的长为10cm，

∴半径OC为4cm，

∴弧BC的长度为＝2π（cm）；

（2）如图②，过点C作CP⊥DH于点P，作CG⊥OB于G，得矩形CGQP，则CP∥OB，

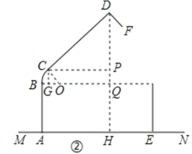
∴∠OCP＝∠BOC＝60°，

∵∠OCD＝90°，

∴∠PCD＝30°，

∴DP＝CD＝×25.2＝12.6（cm），

∵弧BC的长度为2πcm，

∴2π＝，

∴OB＝OC＝6cm，

∴CG＝OCsin60°＝6×＝3≈5.2（cm），

∴DH＝DP+CG+AB＝12.6+5.2+10＝27.8（cm），

故顶端D到桌面MN的距离是27.8cm．