题目内容
【题目】如图,在△ABC中,∠C=90°,D为边BC上一点,E为边AB的中点,过点A作AF∥BC,交DE的延长线于点F,连结BF.
(1)求证:四边形ADBF是平行四边形;
(2)当D为边BC的中点,且BC=2AC时,求证:四边形ACDF为正方形.

【答案】(1)见解析;(2)见解析.
【解析】
(1)根据平行线的性质得到∠AFE=∠BDE,根据全等三角形的性质得到AF=BD,于是得到结论;
(2)首先证明四边形ACDF是矩形,再证明CA=CD即可解决问题;
(1)证明:∵AF∥BC,
∴∠AFE=∠BDE,
在△AEF与△BED中,
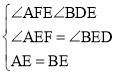 ,
,
∴△AEF≌△BED,
∴AF=BD,
∵AF∥BD,
∴四边形ADBF是平行四边形;
(2)解:∵CD=DB,AE=BE,
∴DE∥AC,
∴∠FDB=∠C=90°,
∵AF∥BC,
∴∠AFD=∠FDB=90°,
∴∠C=∠CDF=∠AFD=90°,
∴四边形ACDF是矩形,
∵BC=2AC,CD=BD,
∴CA=CD,
∴四边形ACDF是正方形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】小明上周零花钱使用情况:(规定:超过50元记为正,少于50元记为负)
星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
+11 | +10 | ﹣17 | +18 | ﹣12 |
请你解答以下问题:
(1)上星期五小明用了多少零花钱;
(2)上星期四比上星期三多花了多少零花钱;
(3)求上周平均每天用多少钱?