��Ŀ����
����Ŀ����ͼ����������![]() ���ʾ��
���ʾ��![]() ��
��![]() ���ʾ��
���ʾ��![]() ��
��![]() ���ʾ��
���ʾ��![]() ����֪��
����֪��![]() ����С������������
����������������![]() ��
��![]() ����
����![]() ��
��
![]()
��1��![]() ��
��![]() ��
��![]() ��
��
��2�����������۵���ʹ�õ�![]() ���
���![]() �غϣ����
�غϣ����![]() ���� ��ʾ�ĵ��غϣ�
���� ��ʾ�ĵ��غϣ�
��3����![]() ��
��![]() ��
��![]() ��ʼ���������˶�������
��ʼ���������˶�������![]() ��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����
��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����![]() �͵�
�͵�![]() �ֱ���ÿ��2����λ���Ⱥ�4����λ���ȵ��ٶ������˶�������
�ֱ���ÿ��2����λ���Ⱥ�4����λ���ȵ��ٶ������˶�������![]() ���ӹ�������
���ӹ�������![]() ���
���![]() ֮��ľ����ʾΪ
֮��ľ����ʾΪ![]() ����
����![]() ���
���![]() ֮��ľ����ʾΪ
֮��ľ����ʾΪ![]() ����
����![]() ���
���![]() ֮��ľ����ʾΪ
֮��ľ����ʾΪ![]() ����
����![]() ��
��![]() ��
��![]() �ij����ú�
�ij����ú�![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
��4���ڣ�3���������£�![]() ��ֵ�Ƿ�����ʱ��
��ֵ�Ƿ�����ʱ��![]() �ı仯���ı䣿���ı䣬��˵�����ɣ������䣬������ֵ��
�ı仯���ı䣿���ı䣬��˵�����ɣ������䣬������ֵ��
���𰸡���1��-2��1��7����2��4����3��![]() ��
��![]() ��
��![]() ����4�����䣮
����4�����䣮![]() .
.
��������
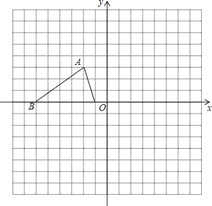
��1������![]() ����a+2=0��c-7=0�����a��c��ֵ����b����С�����������ɵ�b=1����2��������ԳƵ㣬���ɵó��������3�����ݸ�����˶��ٶȺ��˶�����ʾ��t���A,B,C��������ʾ������Ȼ��������������֮��ľ��룻��4������
����a+2=0��c-7=0�����a��c��ֵ����b����С�����������ɵ�b=1����2��������ԳƵ㣬���ɵó��������3�����ݸ�����˶��ٶȺ��˶�����ʾ��t���A,B,C��������ʾ������Ȼ��������������֮��ľ��룻��4������![]() ��ֵ����������t�أ�������⣮
��ֵ����������t�أ�������⣮
��1����![]() ����
����![]() ��
��![]() �����
�����![]() ��
��![]() ��
��
��![]() ����������������
����������������![]() ��
��
�ʴ�Ϊ��-2��1��7��
��2��![]() ��
��
�ԳƵ�Ϊ![]() ��
��![]() ��
��
�ʴ�Ϊ��4��
�������֪��t���Ӻ�A���ʾ-2-t,B���ʾ1+2t��C���ʾ7+4t
��![]() ��
��
![]() ��
��
![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ��
��![]() ��
��
��4�����䣮
![]() .
.
�����t�أ�����![]() ��ֵ������ʱ��
��ֵ������ʱ��![]() �ı仯���ı�.
�ı仯���ı�.