题目内容
【题目】平面直角坐标系 ![]() 中,
中, ![]() 是坐标原点。已知A(0,
是坐标原点。已知A(0, ![]() ),B(1,0),C(6,
),B(1,0),C(6, ![]() ),有一抛物线恰好经过这三点.
),有一抛物线恰好经过这三点.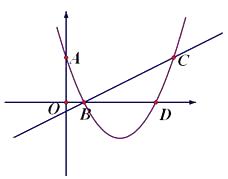
(1)求该抛物线解析式;
(2)若抛物线交 ![]() 轴的另一交点为D,那么抛物线上是否存在一点P,使得
轴的另一交点为D,那么抛物线上是否存在一点P,使得 ![]() ,若存在,求出P的坐标,若不存在,请说明理由。
,若存在,求出P的坐标,若不存在,请说明理由。
【答案】
(1)解:依题可设抛物线解析式为: y=ax2+bx+c(a≠0) ,
∵抛物线经过A,B,C三点,
∴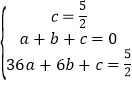 ,
,
∴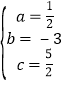 ,
,
∴该抛物线解析式为: y=![]() x23x+
x23x+![]() .
.
(2)解:设直线BC解析式为:y=kx+b,
又∵B(1,0),C(6, ![]() ),
),
∴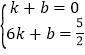 ,
,
∴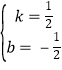 ,
,
∴直线BC的函数解析式为: y=![]() x
x![]() .
.
①若点P在x轴上方,则 OP ∥BC,则OP的函数解析式为 y=![]() x ,
x ,
∴ ,
,
解得 x=![]() ,
,
∴P1(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ) .
) .
②若点P在x轴下方,则OP的函数解析式为 y=![]() x ,
x ,
∴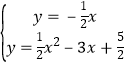 ,
,
解得 x=![]() ,
,
∴ P3(![]() ,
,![]() ),P4(
),P4(![]() ,
,![]() ) .
) .
综上所述: P1(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ) , P3(
) , P3(![]() ,-
,-![]() ),P4(
),P4(![]() ,
,![]() ).
).
【解析】(1)依题可设抛物线解析式为: y=ax2+bx+c(a≠0) ,将A,B,C三点坐标代入抛物线解析式,得到一个三元一次方程组,解之即可求出抛物线解析式.
(2)设直线BC解析式为:y=kx+b,将B(1,0),C(6, ![]() )两点坐标代入,得到一个二元一次方程组,解之即可得到直线BC的解析式;再分两种情况讨论:①若点P在x轴上方,则 OP ∥BC,则OP的函数解析式为 y=
)两点坐标代入,得到一个二元一次方程组,解之即可得到直线BC的解析式;再分两种情况讨论:①若点P在x轴上方,则 OP ∥BC,则OP的函数解析式为 y=![]() x ,②若点P在x轴下方,则OP的函数解析式为 y=
x ,②若点P在x轴下方,则OP的函数解析式为 y=![]() x ,分别将OP直线方程和抛物线联立解出P点坐标即可.
x ,分别将OP直线方程和抛物线联立解出P点坐标即可.
【考点精析】通过灵活运用确定一次函数的表达式,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法即可以解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】某年级共有300名学生,为了解该年级学生在![]() ,
,![]() 两个体育项目上的达标情况,进行了抽样调査.过程如下,请补充完整.
两个体育项目上的达标情况,进行了抽样调査.过程如下,请补充完整.
收集数据从该年级随机抽取30名学生进行测试,测试成绩(百分制)如下:
![]() 项目 78 86 74 81 75 76 87 49 74 91 75 79 81 71 74 81 86 69 83 77 82 85 92 95 58 54 63 67 82 74
项目 78 86 74 81 75 76 87 49 74 91 75 79 81 71 74 81 86 69 83 77 82 85 92 95 58 54 63 67 82 74
![]() 项目 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 100 70 40 84 86 92 96 53 57 63 68 81 75
项目 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 100 70 40 84 86 92 96 53 57 63 68 81 75
整理、描述数据
![]() 项目的频数分布表
项目的频数分布表
分组 | 划记 | 频数 |
| — | 1 |
|
| 2 |
|
| 2 |
|
| 8 |
| ||
|
| 5 |
(说明:成绩80分及以上为优秀,60~79分为基本达标,59分以下为不合格)
根据以上信息,回答下列问题:
(1)补全统计图、统计表;
(2)在此次测试中,成绩更好的项目是__________,理由是__________;
(3)假设该年级学生都参加此次测试,估计![]() 项目和
项目和![]() 项目成绩都是优秀的人数最多为________人.
项目成绩都是优秀的人数最多为________人.