ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§ΫΪΝΫΗωΆξ»ΪœύΆ§ΒΡ»ΐΫ«–Έ÷ΫΤ§![]() ΚΆ
ΚΆ![]() ÷ΊΚœΖ≈÷ΟΘ§Τδ÷–
÷ΊΚœΖ≈÷ΟΘ§Τδ÷–![]() Θ§
Θ§![]() Θ°
Θ°
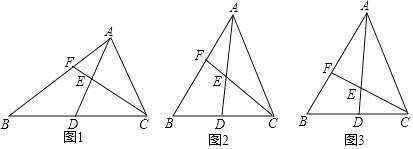
Θ®1Θ©≤ΌΉςΖΔœ÷
»γΆΦ2Θ§ΙΧΕ®![]() Θ§ Ι
Θ§ Ι![]() »ΤΒψ
»ΤΒψ![]() –ΐΉΣΘ§Β±Βψ
–ΐΉΣΘ§Β±Βψ![]() «ΓΚΟ¬δ‘Ύ
«ΓΚΟ¬δ‘Ύ![]() ±Ώ…œ ±Θ§ΧνΩ’ΘΚ
±Ώ…œ ±Θ§ΧνΩ’ΘΚ
ΔΌœΏΕΈ![]() ”κ
”κ![]() ΒΡΈΜ÷ΟΙΊœΒ «______ΘΜ
ΒΡΈΜ÷ΟΙΊœΒ «______ΘΜ
ΔΎ…η![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() Θ§
Θ§![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() Θ§‘ρ
Θ§‘ρ![]() ”κ
”κ![]() ΒΡ ΐΝΩΙΊœΒ «______
ΒΡ ΐΝΩΙΊœΒ «______
Θ®2Θ©≤¬œκ¬έ÷Λ
Β±![]() »ΤΒψ
»ΤΒψ![]() –ΐΉΣΒΫ»γΆΦ3Υυ ΨΒΡΈΜ÷Ο ±Θ§–ΓΟς≤¬œκ1Θ°÷–
–ΐΉΣΒΫ»γΆΦ3Υυ ΨΒΡΈΜ÷Ο ±Θ§–ΓΟς≤¬œκ1Θ°÷–![]() ”κ
”κ![]() ΒΡ ΐΝΩΙΊœΒ»‘»Μ≥…ΝΔΘ§≤Δ≥Δ ‘Ζ÷±πΉς≥ωΝΥ
ΒΡ ΐΝΩΙΊœΒ»‘»Μ≥…ΝΔΘ§≤Δ≥Δ ‘Ζ÷±πΉς≥ωΝΥ![]() ΚΆ
ΚΆ![]() ÷–
÷–![]() ΓΔ
ΓΔ![]() ±Ώ…œΒΡΗΏΘ§«κΡψ÷ΛΟς–ΓΟςΒΡ≤¬œκΘ°
±Ώ…œΒΡΗΏΘ§«κΡψ÷ΛΟς–ΓΟςΒΡ≤¬œκΘ°
Θ®3Θ©ΆΊ’ΙΧΫΨΩ
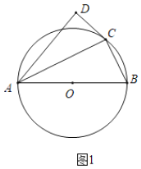
“―÷ΣΓœABC=60ΓψΘ§Βψ![]() «Ϋ«ΤΫΖ÷œΏ…œ“ΜΒψΘ§
«Ϋ«ΤΫΖ÷œΏ…œ“ΜΒψΘ§![]() Θ§
Θ§![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() (»γΆΦ4)Θ°»τ‘Ύ…δœΏ
(»γΆΦ4)Θ°»τ‘Ύ…δœΏ![]() …œ¥φ‘ΎΒψ
…œ¥φ‘ΎΒψ![]() Θ§ Ι
Θ§ Ι![]() Θ§«κ«σ≥ωœύ”ΠΒΡ
Θ§«κ«σ≥ωœύ”ΠΒΡ![]() ΒΡ≥ΛΘ°
ΒΡ≥ΛΘ°
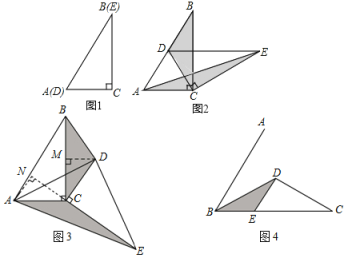
ΓΨ¥πΑΗΓΩΘ®1Θ©≤ΌΉςΖΔœ÷ΘΚΔΌDEΓΈACΘΜΔΎ![]() =
=![]() ΘΜΘ®2Θ©≤¬œκ¬έ÷ΛΘΚ
ΘΜΘ®2Θ©≤¬œκ¬έ÷ΛΘΚ![]() =
=![]() »‘»Μ≥…ΝΔΘ§÷ΛΟςΦϊΫβΈωΘΜΘ®3Θ©ΆΊ’ΙΧΫΨΩΘΚ
»‘»Μ≥…ΝΔΘ§÷ΛΟςΦϊΫβΈωΘΜΘ®3Θ©ΆΊ’ΙΧΫΨΩΘΚ![]() =
=![]() Μρ
Μρ![]()
ΓΨΫβΈωΓΩ
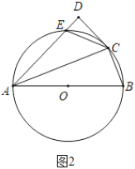
Θ®1Θ©≤ΌΉςΖΔœ÷ΘΚΔΌΗυΨί÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ Φ¥Ω…«σ≥ωΓœEDCΘ§»ΜΚσ÷Λ≥ωΓςCADΈΣΒ»±Ώ»ΐΫ«–ΈΩ…ΒΟΓœDCA=60ΓψΘ§¥”ΕχΒΟ≥ωΓœEDC=ΓœDCAΘ§»ΜΚσΗυΨίΤΫ––œΏΒΡ≈–Ε®Φ¥Ω…ΒΟ≥ωΫα¬έΘΜ
ΔΎΗυΨίΤΫ––œΏ÷°ΦδΒΡΨύάκ¥Π¥ΠœύΒ»ΚΆΆ§ΒΉΒ»ΗΏΩ…ΒΟSΓςDAC=![]() Θ§»ΜΚσΗυΨί30ΓψΥυΕ‘ΒΡ÷±Ϋ«±Ώ «–±±ΏΒΡ“ΜΑκΚΆΒ»±Ώ»ΐΫ«–ΈΒΡ–‘÷ Ω…ΒΟΒψDΈΣABΒΡ÷–ΒψΘ§¥”Εχ÷Λ≥ωSΓςDAC=
Θ§»ΜΚσΗυΨί30ΓψΥυΕ‘ΒΡ÷±Ϋ«±Ώ «–±±ΏΒΡ“ΜΑκΚΆΒ»±Ώ»ΐΫ«–ΈΒΡ–‘÷ Ω…ΒΟΒψDΈΣABΒΡ÷–ΒψΘ§¥”Εχ÷Λ≥ωSΓςDAC=![]() Θ§Φ¥Ω…ΒΟ≥ωΫα¬έΘΜ
Θ§Φ¥Ω…ΒΟ≥ωΫα¬έΘΜ
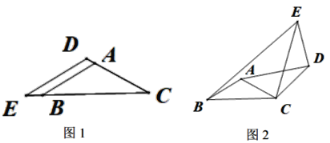
Θ®2Θ©≤¬œκ¬έ÷ΛΘΚάϊ”ΟAAS÷Λ≥ωΓςACNΓ’ΓςDCMΘ§Φ¥Ω…ΒΟ≥ωAN=DMΘ§»ΜΚσΗυΨί–ΐΉΣΒΡ–‘÷ Ω…ΒΟEC=BCΘ§»ΜΚσΗυΨίΝΫΗω»ΐΫ«–ΈΒ»ΒΉΒ»ΗΏΦ¥Ω…ΒΟ≥ωΫα¬έΘΜ
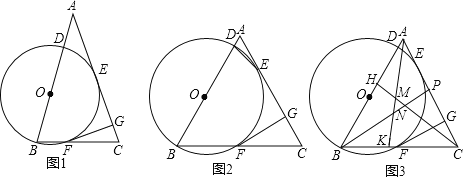
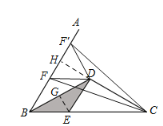
Θ®3Θ©ΆΊ’ΙΧΫΨΩΘΚ―”≥ΛCDΫΜAB”ΎΒψHΘ§ΙΐΒψEΉςEGΓΆBD”ΎGΘ§άϊ”Ο30ΓψΥυΕ‘ΒΡ÷±Ϋ«±Ώ «–±±ΏΒΡ“ΜΑκΚΆΙ¥Ι…Ε®άμΖ÷±π«σ≥ωBHΚΆGEΘ§»ΜΚσΗυΨίΒψFΒΡΈΜ÷ΟΖ÷άύΧ÷¬έΘ§ΗυΨίΝΫΗω»ΐΫ«–ΈΒΡΟφΜΐœύΒ»ΓΔΒΉœύΒ»Ρ«Ο¥ΗΏ“≤œύΒ»Φ¥Ω…«σ≥ωFHΘ§¥”ΕχΖ÷±π«σ≥ωBFΒΡ≥Λ
ΫβΘΚΘ®1Θ©≤ΌΉςΖΔœ÷ΘΚΔΌDEΓΈACΘ§άμ”…»γœ¬ΘΚ
ΓΏ![]() Θ§
Θ§![]() Θ°
Θ°
ΓύΓœBAC=90ΓψΘ≠ΓœB=60ΓψΘ§ΓœEDC=90ΓψΘ≠ΓœDEC=60Γψ
ΓΏΒψ![]() «ΓΚΟ¬δ‘Ύ
«ΓΚΟ¬δ‘Ύ![]() ±Ώ…œ ±Θ§
±Ώ…œ ±Θ§
ΓύCA=CD
ΓύΓςCADΈΣΒ»±Ώ»ΐΫ«–Έ
ΓύΓœDCA=60Γψ
ΓύΓœEDC=ΓœDCA
ΓύDEΓΈAC
Ι ¥πΑΗΈΣΘΚDEΓΈACΘ°
ΔΎ![]() =
=![]() Θ§άμ”…»γœ¬
Θ§άμ”…»γœ¬
ΓΏDEΓΈAC
ΗυΨίΤΫ––œΏ÷°ΦδΒΡΨύάκ¥Π¥ΠœύΒ»
ΓύSΓςDAC=![]()
‘ΎRtΓςABC÷–Θ§ΓœB=30Γψ
ΓύAB=2AC
ΓΏΓςCADΈΣΒ»±Ώ»ΐΫ«–Έ
ΓύAC=AD
ΓύAB=2AD
ΓύΒψDΈΣABΒΡ÷–Βψ
ΓύSΓςDAC=![]()
Γύ![]() =
=![]()
Ι ¥πΑΗΈΣΘΚ![]() =
=![]() Θ°
Θ°
Θ®2Θ©≤¬œκ¬έ÷ΛΘΚ![]() =
=![]() »‘»Μ≥…ΝΔΘ§÷ΛΟς»γœ¬
»‘»Μ≥…ΝΔΘ§÷ΛΟς»γœ¬
ΓΏANΓΔDMΖ÷±π «ΓςACEΓΔΓςBCD±Ώ…œΒΡΗΏ
ΓύΓœANC=ΓœDMC=90Γψ
ΓΏΓœACNΘΪΓœNCB=90ΓψΘ§ΓœDCMΘΪΓœNCB=90Γψ
ΓύΓœACN=ΓœDCM
‘ΎΓςACNΚΆΓςDCM÷–
ΓύΓςACNΓ’ΓςDCM
ΓύAN=DM
ΓΏEC=BC
ΓύΓςACEΚΆΓςBCD»¹»ǿ
Γύ![]() =
=![]()
Θ®3Θ©ΆΊ’ΙΧΫΨΩΘΚ―”≥ΛCDΫΜAB”ΎΒψHΘ§ΙΐΒψEΉςEGΓΆBD”ΎGΘ§
ΓΏΓœABC=60ΓψΘ§Βψ![]() «Ϋ«ΤΫΖ÷œΏ…œ“ΜΒψΘ§
«Ϋ«ΤΫΖ÷œΏ…œ“ΜΒψΘ§![]() Θ§
Θ§
ΓύΓœHBD=ΓœCBD=![]() ΓœABC=30Γψ
ΓœABC=30Γψ
ΓΏ![]()
ΓύΓœDCB=ΓœDBC=30Γψ
ΓύΓœBHC=180ΓψΘ≠ΓœHBCΘ≠ΓœDCB=90Γψ
‘ΎRtΓςBDH÷–Θ§HD=![]() Θ§BH=
Θ§BH=![]()
ΓΏ![]()
ΓύΓœEDB=ΓœHBD=30Γψ
ΓύΓœEBD=ΓœEDB
ΓύEB=ED
ΓύBG=![]() =2
=2
‘ΎRtΓςBEG÷–Θ§…ηGE=xΘ§BE=2GE=2x
ΗυΨίΙ¥Ι…Ε®άμΩ…ΒΟΘΚGE2ΘΪBG2=BE2
Φ¥x 2ΘΪ22=Θ®2xΘ©2
ΫβΒΟΘΚx=![]()
ΓύGE=![]()
Θ®iΘ©Β±ΒψF‘ΎœΏΕΈBH…œ ±Θ§
ΓΏ![]() Θ§
Θ§![]()
ΓύFH=GE=![]()
ΓύBF=BHΘ≠FH=![]() ΘΜ
ΘΜ
Θ®iiΘ©Β±![]() ‘ΎœΏΕΈBHΒΡ―”≥ΛœΏ…œ ±
‘ΎœΏΕΈBHΒΡ―”≥ΛœΏ…œ ±
Ά§άμΩ…ΒΟ![]() H= GE=
H= GE=![]()
ΓύB![]() =BHΘΪ
=BHΘΪ![]() H=
H=![]()
Ήέ…œΥυ ωΘΚ![]() =
=![]() Μρ
Μρ![]()

 ΜΤΗ‘–ΓΉ¥‘ΣΫβΨωΈ ΧβΧλΧλΝΖœΒΝ–¥πΑΗ
ΜΤΗ‘–ΓΉ¥‘ΣΫβΨωΈ ΧβΧλΧλΝΖœΒΝ–¥πΑΗ »ΐΒψ“Μ≤βΩλά÷÷ήΦΤΜ°œΒΝ–¥πΑΗ
»ΐΒψ“Μ≤βΩλά÷÷ήΦΤΜ°œΒΝ–¥πΑΗ