题目内容
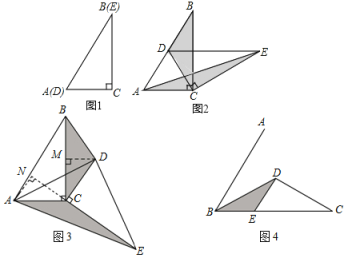
【题目】已知:在△ABC中,AB=AC,点D是AB上一点,以BD为直径的⊙0与AC边相切于点E,交BC于点F,FG⊥AC于点G.
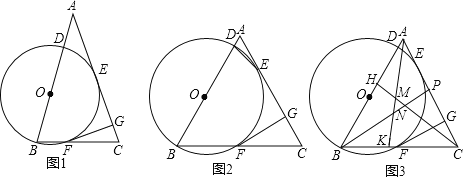
(1)如图l,求证:GE=GF;
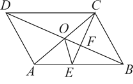
(2)如图2,连接DE,∠GFC=2∠AED,求证:△ABC为等边三角形;
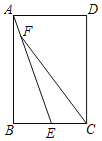
(3)如图3,在(2)的条件下,点H、K、P分别在AB、BC、AC上,AK、BP分别交CH于点M、N,AH=BK,∠PNC﹣![]() ∠BAK=60°,CN=6,CM=4
∠BAK=60°,CN=6,CM=4![]() ,求BC的长.
,求BC的长.
【答案】(1)见解析;(2)见解析;(3)BC=10.
【解析】
(1)由切线的定义得到直角条件,由半径相等可证OFGE为正方形;
(2)由圆周角定理可得直角条件,由2倍角关系可得60°条件,从而证明等边三角形;
(3)结合(2)的结论和条件中角的关系,需要设置角参数,标识图形从而发现BC=BR,用勾股定理建立方程关系,求解方程即可.
解:(1)如图1,连接OE和OF
∵AC是⊙O的切线
∴OE⊥AC,
∴∠OEG=90°
∵FG⊥AC,
∴∠FGE=90°
∵AB=AC,
∴∠ABC=∠ACB
∵OB=OF,
∴∠OBF=∠OFB
∴∠OFB=∠ACB,
∴OF∥AC
∴∠OFG+∠FGE=180°,
∴∠OFG=90°
∴∠OFG=∠FGE=∠OEG=90°
∴四边形OFGE为矩形
∵OF=OE,
∴四边形OFGE为正方形
∴GE=GF
(2)如图2,连接OE,BE
∵BD是⊙O的直径,
∴∠BED=90°
∴∠OED+∠OEB=90°
∵∠OEG=90°,
∴∠AED+∠OED=90°
∵∠OEG=90°,
∴∠AED+∠OED=90°
∴∠OEB=∠AED
∵OB=OE,
∴∠OBE=∠OEB
∴∠OBE=∠AED
∴∠AOE=2∠OEB=2∠AED
∵∠GFC=2∠AED
∴∠AOE=∠GFC
∵∠C+∠GFC=90°,∠A+∠AOE=90°
∴∠C=∠A
∴BA=BC,
∵AB=AC
∴AB=AC=BC
∴△ABC为等边三角形
(3)∵△ABC为等边三角形
∴∠CAH=∠ABK=60°
∵AH=BK,AC=AB,
∴△CAH≌△ABK(SAS)
∴∠ACH=∠BAK
∵∠KMC=∠KAC+∠ACM
∴∠KMC=∠KAC+∠BAK=60°
过点C作CQ⊥AK,垂足为Q,过点B作BT⊥CH,垂足为T
∴∠AQC=∠CTB=90°
∵∠QAC=∠BAC﹣∠BAK=60°,∠TCB=∠ACB﹣∠ACH=60°﹣∠ACH
∴∠QAC=∠TCB,
∵AC=BC
∴△AQC≌△CTB(AAS)
∴QC=BT
在Rt△MQC中,
∵CM=4![]() ,∠QMC=60°,sin∠QMC=
,∠QMC=60°,sin∠QMC=![]()
∴QC=6
设∠BAK=2α=∠ACH
∵∠PNC﹣![]() ∠BAK=60°,
∠BAK=60°,
∴∠PNC=60°+α=∠BNH
∴∠BCH=∠ACB﹣∠ACH=60°﹣2α
延长NH到点R,使RT=TN,连接BR
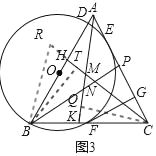
∴BT使RN的垂直平分线
∴BR=BN
∴∠BNR=∠BRN=60°+α
∴∠CBR=180°﹣∠BCR﹣∠CRB=60°+α
∴∠CBR=∠CRB=60°+α
∴BC=RC
设TN=RT=a,
∵CN=6
∴CT=a+6,CR=CB=2a+6
∵CQ=BT=6
在Rt△BTC中
BT2+TC2=BC2
∴62+(a+6)2=(2a+6)2
∴a1=﹣6(舍),a2=2
∴TN=2
∴BC=10

 阅读快车系列答案
阅读快车系列答案【题目】某校九年级(1)班全体学生2018年初中毕业体育学业考试成绩统计表如下:
成绩/分 | 45 | 49 | 52 | 54 | 55 | 58 | 60 |
人数 | 2 | 5 | 6 | 6 | 8 | 7 | 6 |
根据上表中信息判断,下列结论中错误的是( )
A.该班一共有40名同学
B.该班学生这次考试成绩的众数是55分
C.该班学生这次考试成绩的中位数是55分
D.该班学生这次考试成绩的平均数是55分