题目内容
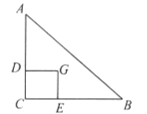
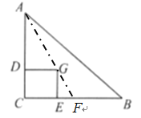
【题目】如图，在
中，
，过重心
作
、
的垂线，垂足分别为
、
，则四边形
的面积与的面积之比为（ ）
A.
B.
C.
D.
【答案】C
【解析】
连接AG并延长交BC于点F，根据G为重心可知，AG=2FG，CF=BF，再证明△ADG∽△GEF，得出
，设矩形CDGE中，DG=a，EG=b，用含a,b的式子将AC，BC的长表示出来，再列式化简即可求出结果．
解：连接AG并延长交BC于点F，根据G为重心可知，AG=2FG，CF=BF，
易得四边形GDCE为矩形，
∴DG∥BC，DG=CD=EG=CE，∠CDG=∠CEG=90°，
∴∠AGD=∠AFC，∠ADG=∠GEF=90°，
∴△ADG∽△GEF，
∴
．
设矩形CDGE中，DG=a，EG=b，
∴AC=AD+CD=2EG+EG=3b，
BC=2CF=2(CE+EF)=2(DG+
)=3a，
∴
．
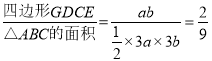故选：C．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
