题目内容
【题目】某超市销售一种文具,进价为 5(元/件),售价为6(元/件)时,当天的销售量为100件,在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件,设当天销售单价统一为![]() (元/件)(
(元/件)(![]() ,且
,且![]() 是按0.5元的倍数上涨),当天销售利润为
是按0.5元的倍数上涨),当天销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价的范围;
(3)若每件文具的利润不超过60%,要使当天获得利润最大,每件文具售价为多少元?并求出最大利润.
【答案】(1)![]() ;(2)当天销售单价所在的范围为
;(2)当天销售单价所在的范围为![]() ;(3)每件文具售价为8元时,最大利润为240元.
;(3)每件文具售价为8元时,最大利润为240元.
【解析】
(1)根据当天销售利润等于每件利润乘以当天销量,找到当天销量与单价的关系即可得出答案;
(2)先求出利润等于240元时的单价,再根据二次函数图像的性质确定范围;
(3)先确定单价的范围,再根据二次函数的性质求最值.
(1)由题意![]()
∴![]() 与
与![]() 的函数关系式为:
的函数关系式为:![]()
(2)要使当天利润不低于240元,则![]() .
.
![]()
解得,![]() ,
,![]()
![]()
![]() ,抛物线的开口向下,
,抛物线的开口向下,
![]() 当天销售单价所在的范围为
当天销售单价所在的范围为![]()
(3)![]() 每件文具利润不超过60%
每件文具利润不超过60%
![]() ,得
,得![]()
![]() 文具的销售单价为
文具的销售单价为![]()
由(1)得![]()
![]() 对称轴为
对称轴为![]()
![]()
![]() 在对称轴的左侧,且
在对称轴的左侧,且![]() 随着
随着![]() 的增大而增大
的增大而增大
![]() 当
当![]() 时,取得最大值,此时
时,取得最大值,此时![]() ,
,
即每件文具售价为8元时,最大利润为240元.

练习册系列答案
相关题目
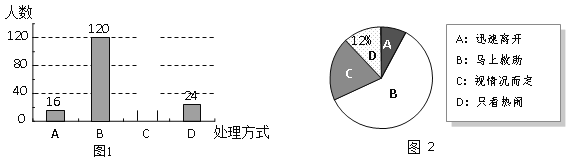
【题目】某校组织了2000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:
成绩 | 频数 | 频率 |
| 20 |
|
| 16 | 0.08 |
|
| 0.15 |
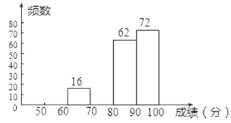
请你根据以上的信息,回答下列问题:
(1)![]() ,
,![]() ;
;
(2)在扇形统计图中,“成绩![]() 满足
满足![]() ”对应扇形的圆心角的度数是 ;
”对应扇形的圆心角的度数是 ;
(3)若将得分转化为等级,规定:![]() 评为
评为![]() ,
,![]() 评为
评为![]() ,
,![]() 评为
评为![]() ,
,![]() 评为
评为![]() .这次全校参加竞赛的学生约有 人参赛成绩被评为“
.这次全校参加竞赛的学生约有 人参赛成绩被评为“![]() ”.
”.