题目内容
【题目】知识背景：
当a＞0且x＞0时，因为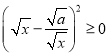
，所以x﹣2
≥0，从而
（当
，即x＝
时取等号）．
设函数y＝x+
（x＞0，a＞0），由上述结论可知：当x＝时，该函数有最小值2．
应用举例
已知函数为y1＝x（x＞0）与函数y2＝
（x＞0），则当x＝
时，y1+y2＝x+有最小值为2．
解决问题
（1）已知函数为y1＝x﹣1（x＞1）与函数y2＝（x﹣1）2+9（x＞1），当x取何值时，
有最小值？最小值是多少？
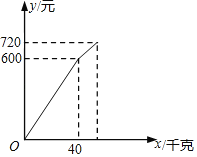
（2）已知某设备租赁使用成本包含以下三部分：一是设备的安装调试费用，共490元；二是设备的租赁使用费用，每天200元；三是设备的折旧费用，它与使用天数的平方成正比，比例系数为0．001．若设该设备的租赁使用天数为x天，则当x取何值时，该设备平均每天的租赁使用成本最低？最低是多少元？
【答案】（1）x＝4时
有最小值，最小值是6；（2）当x取700时，该设备平均每天的租赁使用成本最低，最低是201.4元．
【解析】
（1）通过对知识背景和应用举例的理解来解决即可；
（2）平均每天租赁使用成本＝总成本÷总使用天数，先根据成本包括的三部分把总成本表示出来，然后除以总使用天数，根据知识背景即可求解．
（1）＝
＝（x﹣1）+
∵x＞1，∴x﹣1＞0
根据题意，当x﹣1＝
＝3时，
有最小值2＝6，
∴x＝4，
即x＝4时有最小值，最小值是6；
（2）设该设备平均每天的租赁使用成本w元，
根据题意，得
w＝（490+200x+0.001x2）÷x
＝
+200+0.001x
所以当＝0.001x时，w有最小值，
w最小值为2
+200＝201.4．
解得x＝700或﹣700（舍去），
答：当x取700时，该设备平均每天的租赁使用成本最低，最低是201.4元．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
