题目内容
【题目】观察下列等式
12=1= ![]() ×1×2×(2+1)
×1×2×(2+1)
12+22= ![]() ×2×3×(4+1)
×2×3×(4+1)
12+22+32= ![]() ×3×4×(6+1)
×3×4×(6+1)
12+22+32+42= ![]() ×4×5×(8+1)…
×4×5×(8+1)…
可以推测12+22+32+…+n2= .
【答案】![]()
n(n+1)(2n+1)
【解析】解:∵第1个等式:12=1= ![]() ×1×2×(2×1+1);
×1×2×(2×1+1);
第2个等式:12+22= ![]() ×2×3×(2×2+1);
×2×3×(2×2+1);
第3个等式:12+22+32= ![]() ×3×4×(2×3+1)
×3×4×(2×3+1)
第4个等式:12+22+32+42= ![]() ×4×5×(2×4+1)
×4×5×(2×4+1)
…
∴第n个等式:12+22+32+…+n2= ![]() n(n+1)(2n+1),
n(n+1)(2n+1),
所以答案是: ![]() n(n+1)(2n+1).
n(n+1)(2n+1).
【考点精析】利用数与式的规律对题目进行判断即可得到答案,需要熟知先从图形上寻找规律,然后验证规律,应用规律,即数形结合寻找规律.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
【题目】如图,是某广场台阶(结合轮椅专用坡道)景观设计的模型,以及该设计第一层的截面图,第一层有十级台阶,每级台阶的高为0.15米,宽为0.4米,轮椅专用坡道AB的顶端有一个宽2米的水平面BC;《城市道路与建筑物无障碍设计规范》第17条,新建轮椅专用坡道在不同坡度的情况下,坡道高度应符合以下表中的规定:
坡度 | 1:20 | 1:16 | 1:12 |
最大高度(米) | 1.50 | 1.00 | 0.75 |
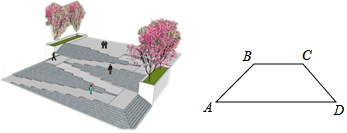
(1)选择哪个坡度建设轮椅专用坡道AB是符合要求的?说明理由;
(2)求斜坡底部点A与台阶底部点D的水平距离AD.