题目内容
【题目】如图,△ABC是等腰三角形,∠C=90°,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化过程中,有下列结论:
①DE=DF;
②∠EDF=90°;
③四边形CEDF不可能为正方形;
④四边形CEDF的面积保持不变.
一定成立的结论有(把你认为正确的序号都填上)
【答案】①②④
【解析】解:①连接CD;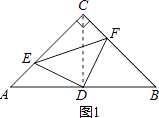
∵△ABC是等腰直角三角形,
∴∠DCB=∠A=45°,CD=AD=DB;
在△ADE和△CDF中,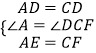
∴△ADE≌△CDF(SAS),
∴ED=DF,①正确;
②∵△ADE≌△CDF,
∴∠CDF=∠EDA,
∵∠ADE+∠EDC=90°,
∴∠EDC+∠CDF=∠EDF=90°,②正确;
③当E、F分别为AC、BC中点时,DE⊥AC,DF⊥BC,又∠ACB=90°,
∴四边形CEDF是矩形,
∵CE=CF,
∴四边形CDFE是正方形,③错误;
④如图2,分别过点D,作DM⊥AC,DN⊥BC,于点M,N,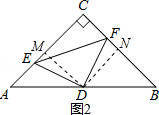
则DM=DN,
在Rt△DME和Rt△DNF中,![]() ,
,
∴Rt△DME≌Rt△DNF(HL),
∴四边形CEDF的面积等于正方形CMDN面积,故面积保持不变,④正确,
所以答案是:①②④.
【考点精析】掌握等腰三角形的性质是解答本题的根本,需要知道等腰三角形的两个底角相等(简称:等边对等角).

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案
相关题目