题目内容
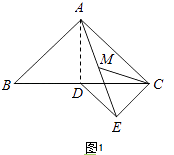
【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF. 
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
【答案】
(1)证明:连接OD,与AF相交于点G,
∵CE与⊙O相切于点D,
∴OD⊥CE,
∴∠CDO=90°,
∵AD∥OC,
∴∠ADO=∠DOC,∠DAO=∠BOC,
∵OA=OD,
∴∠ADO=∠DAO,
∴∠DOC=∠BOC,
在△CDO和△CBO中,
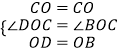 ,
,
∴△CDO≌△CBO,
∴∠CBO=∠CDO=90°,
∴CB是⊙O的切线
(2)解:由(1)可知∠DOA=∠BCO,∠DOC=∠BOC,
∵∠ECB=60°,
∴∠DCO=∠BCO= ![]() ∠ECB=30°,
∠ECB=30°,
∴∠DOC=∠BOC=60°,
∴∠DOA=60°,
∵OA=OD,
∴△OAD是等边三角形,
∴AD=OD=OF,∵∠GOF=∠ADO,
在△ADG和△FOG中,
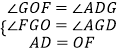 ,
,
∴△ADG≌△FOG,
∴S△ADG=S△FOG,
∵AB=6,
∴⊙O的半径r=3,
∴S阴=S扇形ODF= ![]() =
= ![]() π.
π.
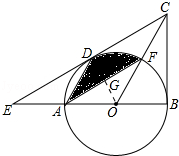
【解析】(1)欲证明CB是⊙O的切线,只要证明BC⊥OB,可以证明△CDO≌△CBO解决问题.(2)首先证明S阴=S扇形ODF , 然后利用扇形面积公式计算即可.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目