题目内容
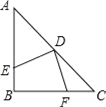
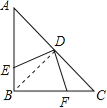
【题目】如图，在等腰三角形ABC中，∠ABC=90°，D为AC边上中点，过D点作DE⊥DF，交AB于E，交BC于F，若S四边形BFDE=9，则AB的长为：
A. 3 B. 6 C. 9 D. 18
【答案】B
【解析】试题分析：首先连接BD，由已知等腰直角三角形ABC，可推出BD⊥AC且BD=CD=AD，∠ABD=45°再由DE丄DF，可推出∠FDC=∠EDB，又等腰直角三角形ABC可得∠C=45°，所以△EDB≌△FDC，所以四边形的面积是三角形ABC的一半，利用三角形的面积公式即可求出AB的长．
解：连接BD，
∵等腰直角三角形ABC中，D为AC边上中点，
∴BD⊥AC（三线合一），BD=CD=AD，∠ABD=45°，
∴∠C=45°，
∴∠ABD=∠C，
又∵DE丄DF，
∴∠FDC+∠BDF=∠EDB+∠BDF，
∴∠FDC=∠EDB，
在△EDB与△FDC中，
∵
，
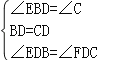∴△EDB≌△FDC（ASA），
∴S四边形面积=S△BDC=
S△ABC=9，
∴AB2=18，
∴AB=6，
故选B．
练习册系列答案
相关题目
