题目内容
【题目】如图,A(﹣![]() ,0),B(﹣
,0),B(﹣![]() ,3),∠BAC=90°,C在y轴的正半轴上.
,3),∠BAC=90°,C在y轴的正半轴上.
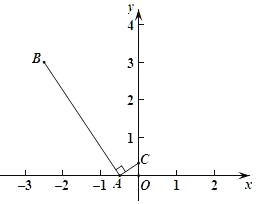
(1)求出C点坐标;
(2)将线段AB沿射线AC向上平移至第一象限,得线段DE,若D、E两点均在双曲线y=![]() 上,
上,
①求k的值;
②直接写出线段AB扫过的面积.
【答案】(1)(0,![]() );(2)①12;②
);(2)①12;②![]()
【解析】
(1)过点B作x轴的垂线,构造三垂直相似模型,由对应边成比例求得OC的长度.
(2)①由平移的性质可知,AB∥DE,AD∥BE,即D、E横纵坐标差与A、B横纵坐标差相等.因为沿射线AC平移,求直线AC的解析式,用d表示点D坐标,再用d表示点E坐标,由D、E在双曲线上,列得关于d、k的方程,进而求得k.
②由平移性质可知四边形ABED是平行四边形,又∠BAC=90°,即为矩形,所以线段AB扫过的面积即为矩形ABED的面积,用两点间距离公式求出AB、AD长度即求出面积.
解:(1)过点B作BH⊥x轴于点H,
∴∠BHA=∠BAC=∠AOC=90°
∴∠B+∠BAH=∠BAH+∠OAC=90°
∴∠B=∠OAC
∴△BAH∽△ACO
∴![]()
∵A(﹣![]() ,0),B(﹣
,0),B(﹣![]() ,3)
,3)
∴OA=![]() ,OH=
,OH=![]() ,BH=3
,BH=3
∴AH=OH﹣OA=![]() =2
=2
∴CO=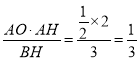
∴点C坐标为(0,![]() )
)
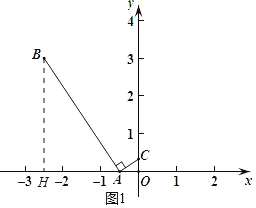
(2)①∵线段AB沿射线AC向上平移至第一象限
∴点A对应点D在直线AC上,AD∥BE,
∴xD﹣xE=xA﹣xB=2,yE﹣yD=yB﹣yA=3
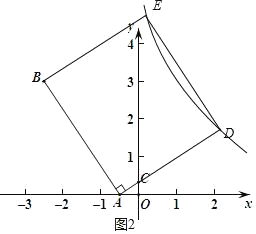
设直线AC解析式为:y=ax+b
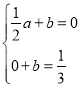 解得:
解得:![]()
∴直线AC解析式为:![]()
设点D坐标为(d,![]() ),
),
则xE=xD﹣2=d﹣2,yE=yD+3=![]()
即点E(d﹣2,![]() )
)
∵点D、E在函数y=![]() 图象上(k>0)
图象上(k>0)
∴![]()
解得:d=4
∴k=4×(![]() ×4+
×4+![]() )=12
)=12
②∵A(﹣![]() ,0),B(﹣
,0),B(﹣![]() ,3),D(4,3)
,3),D(4,3)
∴AB=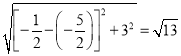 ,AD=
,AD=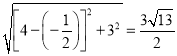
∵AB∥DE,AD∥BE
∴四边形ABED是平行四边形
∵∠BAC=90°
∴ABED是矩形
∴S矩形ABED=ABAD=![]()
∴线段AB扫过的面积为![]()

 课堂全解字词句段篇章系列答案
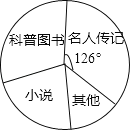
课堂全解字词句段篇章系列答案【题目】2018年东营市教育局在全市中小学开展了“情系疏勒书香援疆”捐书活动,200多所学校的师生踊跃参与,向新疆疏勒县中小学共捐赠爱心图书28.5万余本.某学校学生社团对本校九年级学生所捐图书进行统计,根据收集的数据绘制了下面不完整的统计图表.请你根据统计图表中所提供的信息解答下列问题:
图书种类 | 频数(本) | 频率 |
名人传记 | 175 | a |
科普图书 | b | 0.30 |
小说 | 110 | c |
其他 | 65 | d |
(1)求该校九年级共捐书多少本;
(2)统计表中的a= ,b= ,c= ,d= ;
(3)若该校共捐书1500本,请估计“科普图书”和“小说”一共多少本;
(4)该社团3名成员各捐书1本,分别是1本“名人传记”,1本“科普图书”,1本“小说”,要从这3人中任选2人为受赠者写一份自己所捐图书的简介,请用列表法或树状图求选出的2人恰好1人捐“名人传记”,1人捐“科普图书”的概率.
【题目】二次函数![]() (
(![]() 是常数,
是常数,![]() )的自变量
)的自变量![]() 与函数值
与函数值![]() 的部分对应值如下表:
的部分对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … |
|
|
|
|
| … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②
;②![]() 和3是关于
和3是关于![]() 的方程
的方程![]() 的两个根;③
的两个根;③![]()
![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A. 0B. 1C. 2D. 3