Question

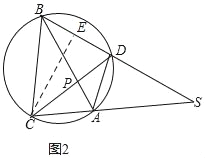
【题目】如图，⊙O中，弦AB、CD相交点P，弦CA、BD的延长线交于S，∠APD＝2m°，∠PAC＝m°+15°．

（1）求∠S的度数；

（2）连AD，BC，若，求m的值．

Answer 1

【答案】(1) 30°;(2) m＝45

【解析】

（1）由圆周角定理可知：∠PAC＝∠PDB＝m°+15°，从而可知∠PDS＝∠PAS，由于∠APD＝2m°，利用四边形内角和即可得出∠S的度数；

（2）过点C作CE⊥BD于点E，由圆内接四边形的性质可知：∠DAS＝∠SBC，从而可证明△SAD∽△SBC，从而可求出ED、CE的长度，从而可得出∠ECD的度数，进而求出m的值．

（1）由圆周角定理可知：∠PAC＝∠PDB＝m°+15°，

∴∠PDS＝∠PAS＝180﹣（m°+15°）＝165°﹣m°，

∵∠APD＝2m°，

∴∠S＝360°﹣∠PDS﹣∠PAS﹣∠APD

＝360°﹣2（165°﹣m°）﹣2m°

＝30°，

（2）过点C作CE⊥BD于点E，

由圆内接四边形的性质可知：∠DAS＝∠SBC，

∵∠S＝∠S，

∴△SAD∽△SBC，

∴，

设SD＝1，SC＝，

∵∠S＝30°，

,

,

,

，

∴∠ECD＝30°，

∴∠EDC＝60°，

∴m°+15°＝60°，

∴m＝45.