题目内容
【题目】如图，在△ABC中，AB=AC=6，∠BAC=120°，点D是AB边上的点， 
= 
，点P为底边BC上的一动点，则△PDA周长的最小值为 ． 
【答案】2 
+2
【解析】解：∵AB=AC=6， 
= 
， ∴AD=2，BD=4，
作A关于BC的对称点A′，连接DA′交BC于P，
则DA′=PD+PA的最小值，
过A′作A′H⊥AB于H，
∵∠BAC=120°，
∴∠BAA′=60°，∠B=∠C=30°，
∴AA′=6，A′H=3 
，
∴DH=3﹣2=1，
∴A′D= 
=2 ，
∴△PDA周长的最小值=2 +2，
所以答案是：2 +2．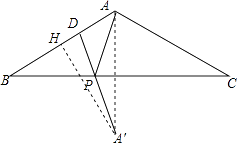
【考点精析】本题主要考查了等腰三角形的性质和含30度角的直角三角形的相关知识点，需要掌握等腰三角形的两个底角相等（简称：等边对等角）；在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半才能正确解答此题．
练习册系列答案
步步高达标卷系列答案
相关题目
