题目内容
【题目】如图，已知斜坡AB长为80米，坡角（即∠BAC）为30°，BC⊥AC，现计划在斜坡中点D处挖去部分坡体（用阴影表示）修建一个平行于水平线CA的平台DE和一条新的斜坡BE．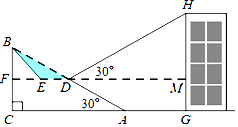
（1）若修建的斜坡BE的坡角为45°，求平台DE的长；（结果保留根号）
（2）一座建筑物GH距离A处36米远（即AG为36米），小明在D处测得建筑物顶部H的仰角（即∠HDM）为30°．点B、C、A、G、H在同一个平面内，点C、A、G在同一条直线上，且HG⊥CG，求建筑物GH的高度．（结果保留根号）
【答案】
（1）
解：∵修建的斜坡BE的坡角为45°，
∴∠BEF=45°，
∵∠DAC=∠BDF=30°，AD=BD=40，
∴BF=EF= 
BD=20，DF= 
，
∴DE=DF﹣EF=20 
﹣20，
∴平台DE的长为（20 ﹣20）米
（2）
解：过点D作DP⊥AC，垂足为P．
在Rt△DPA中，DP= AD= ×40=20，PA=ADcos30°=20 ，
在矩形DPGM中，MG=DP=20，DM=PG=PA+AG=20 +36．
在Rt△DMH中，HM=DMtan30°=（20 +36）× 
=20+12 ，
则GH=HM+MG=20+12 +20=40+12 ．
答：建筑物GH高为（40+12 ）米．
【解析】（1）根据题意得出∠BEF=45°，解直角△BDF，求出BF，DF，进而得出EF的长，即可得出答案；（2）利用在Rt△DPA中，DP= AD，以及PA=ADcos30°进而得出DM的长，利用HM=DMtan30°得出即可．
【考点精析】解答此题的关键在于理解关于仰角俯角问题的相关知识，掌握仰角：视线在水平线上方的角；俯角：视线在水平线下方的角．
阅读快车系列答案
【题目】随着北京公交票制票价调整，公交集团换成了新版公交站牌，乘客在乘车时可以通过新版公交站牌计算乘车费用．新版公交站牌每一个站名上方都有一个对应的数，将上下车站站名所对应数相减取绝对值就是乘车路程，再按照其所在计价区段，参照票制规则计算票价．具体内容如下：
乘车路程计价区段 | 0～10 | 11～15 | 16～20 | … |
对应票价(元) | 2 | 3 | 4 | … |
另外，一卡通普通卡刷卡实行五折优惠，学生卡实行二五折优惠.小明用学生卡乘车，上车时站名上对应的数是5，下车时站名上对应的数是22，那么小明乘车的费用是_____元.
