��Ŀ����
��ͼ��ʾ����ƽ��ֱ������ϵxOy�У�������OABC�ı߳�Ϊ2cm����A��C��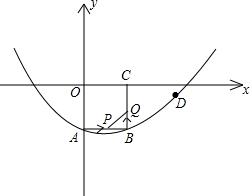 ����y��ĸ������x����������ϣ�������y=ax2+bx+c������A��B��D(4��-
����y��ĸ������x����������ϣ�������y=ax2+bx+c������A��B��D(4��-| 2 |
| 3 |
��1���������ߵĽ���ʽ��
��2�������P�ɵ�A������AB����2cm/s���ٶ����B�˶���ͬ
ʱ��Q�ɵ�B������BC����1cm/s���ٶ����C�˶���������һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶�����S=PQ2��cm2��
�������S���˶�ʱ��t֮��ĺ�����ϵʽ����д��t��ȡֵ��Χ��
�ڵ�Sȡ
| 5 |
| 4 |
��3���������ߵĶԳ��������M��ʹ��M��D��A�ľ���֮����������M�����꣮
��������1���������ߵĽ���ʽ��y=ax2+bx+c�����A��B��D��������뼴�ɣ�
��2�����ɹ��ɶ�������������ڼ�����ڵ�R���ɹ�����P��B��R��QΪ�����ƽ���ı��Σ����P��Q�����꣬�ٷ�Ϊ�����������A��B��C���ɸ���ƽ���ı��ε��������R�����꣮
��3��A���������ߵĶԳ���ĶԳƵ�ΪB����B��D��ֱ���������ߵĶԳ���Ľ���Ϊ����M�����ֱ��BD�Ľ���ʽ���������ߵĶԳ���x=1���뼴�����M�����꣮
��2�����ɹ��ɶ�������������ڼ�����ڵ�R���ɹ�����P��B��R��QΪ�����ƽ���ı��Σ����P��Q�����꣬�ٷ�Ϊ�����������A��B��C���ɸ���ƽ���ı��ε��������R�����꣮
��3��A���������ߵĶԳ���ĶԳƵ�ΪB����B��D��ֱ���������ߵĶԳ���Ľ���Ϊ����M�����ֱ��BD�Ľ���ʽ���������ߵĶԳ���x=1���뼴�����M�����꣮
����⣺��1���������ߵĽ���ʽ��y=ax2+bx+c��
�������εı߳�2��
��B�����꣨2��-2��A��������ǣ�0��-2����
��A��0��-2����B��2��-2����D��4��-
������ã�
��
���a=
��b=-
��c=-2��
�������ߵĽ���ʽΪ��y=
x2-
x-2��
�������ߵĽ���ʽΪ��y=
x2-
x-2��
��2������ͼ��֪��PB=2-2t��BQ=t��
��S=PQ2=PB2+BQ2��
=��2-2t��2+t2��
��S=5t2-8t+4��0��t��1����
��S���˶�ʱ��t֮��ĺ�����ϵʽ��S=5t2-8t+4��t��ȡֵ��Χ��0��t��1��
�ڽ⣺������ڵ�R���ɹ�����P��B��R��QΪ�����ƽ���ı��Σ�
��S=5t2-8t+4��0��t��1����
�൱S=
ʱ��5t2-8t+4=
����20t2-32t+11=0��
���t=
��t=
���������⣬��ȥ����
��ʱ��P������Ϊ��1��-2����Q�������Ϊ��2��-
����
��R����ڣ���������ۣ�
��i������R��BQ���ұߣ���ͼ��1����ʾ����ʱQR=PB��RQ��PB��
��R�ĺ�����Ϊ3��R��������Ϊ-
��
��R��3��-
����
����y=
x2-
x-2������������ȣ�
����ʱ����R��3��-
���������⣻
��ii������R��QB�����ʱ����ʱPR=QB��PR��QB��
��R��1��-
�����룬y=
x2-
x-2��
���Ҳ���ȣ���R�����������ϣ�
��������������һ��R��3��-
���������⣮
����ڣ�R��������ǣ�3��-
����
��3����ͼ��2����M��B=M��A��
��A���������ߵĶԳ���ĶԳƵ�ΪB����B��D��ֱ���������ߵĶԳ���Ľ���Ϊ����M��
�����ǣ���MA=MB����M��ΪL��DB�Ľ��㣬������B��M��D���������Σ�
��|MD|-|MB|��|DB|��
��M��D��A�ľ���֮��Ϊ|DB|ʱ����ֵ���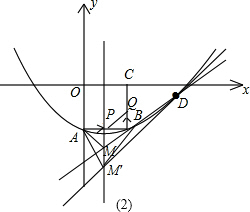
��ֱ��BD�Ľ���ʽ��y=kx+b����B��D���������ã�
��
��ã�k=
��b=-
��
��y=
x-
��
������y=
x2-
x-2�ĶԳ�����x=1��
��x=1����ã�y=-
��M��������1��-
����
��M��������1��-
����
�������εı߳�2��
��B�����꣨2��-2��A��������ǣ�0��-2����
��A��0��-2����B��2��-2����D��4��-
| 2 |
| 3 |
|
���a=
| 1 |
| 6 |
| 1 |
| 3 |
�������ߵĽ���ʽΪ��y=
| 1 |
| 6 |
| 1 |
| 3 |
�������ߵĽ���ʽΪ��y=
| 1 |
| 6 |
| 1 |
| 3 |
��2������ͼ��֪��PB=2-2t��BQ=t��
��S=PQ2=PB2+BQ2��
=��2-2t��2+t2��
��S=5t2-8t+4��0��t��1����
��S���˶�ʱ��t֮��ĺ�����ϵʽ��S=5t2-8t+4��t��ȡֵ��Χ��0��t��1��
�ڽ⣺������ڵ�R���ɹ�����P��B��R��QΪ�����ƽ���ı��Σ�
��S=5t2-8t+4��0��t��1����
�൱S=
| 5 |
| 4 |
| 5 |
| 4 |
���t=
| 1 |
| 2 |
| 11 |
| 10 |
��ʱ��P������Ϊ��1��-2����Q�������Ϊ��2��-
| 3 |
| 2 |
��R����ڣ���������ۣ�
��i������R��BQ���ұߣ���ͼ��1����ʾ����ʱQR=PB��RQ��PB��
��R�ĺ�����Ϊ3��R��������Ϊ-
| 3 |
| 2 |
��R��3��-
| 3 |
| 2 |
����y=
| 1 |
| 6 |
| 1 |
| 3 |
����ʱ����R��3��-
| 3 |
| 2 |
��ii������R��QB�����ʱ����ʱPR=QB��PR��QB��
��R��1��-
| 5 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
���Ҳ���ȣ���R�����������ϣ�
��������������һ��R��3��-
| 3 |
| 2 |

����ڣ�R��������ǣ�3��-
| 3 |
| 2 |
��3����ͼ��2����M��B=M��A��
��A���������ߵĶԳ���ĶԳƵ�ΪB����B��D��ֱ���������ߵĶԳ���Ľ���Ϊ����M��
�����ǣ���MA=MB����M��ΪL��DB�Ľ��㣬������B��M��D���������Σ�
��|MD|-|MB|��|DB|��
��M��D��A�ľ���֮��Ϊ|DB|ʱ����ֵ���

��ֱ��BD�Ľ���ʽ��y=kx+b����B��D���������ã�
|
��ã�k=
| 2 |
| 3 |
| 10 |
| 3 |
��y=
| 2 |
| 3 |
| 10 |
| 3 |
������y=
| 1 |
| 6 |
| 1 |
| 3 |
��x=1����ã�y=-
| 8 |
| 3 |
��M��������1��-
| 8 |
| 3 |
��M��������1��-
| 8 |
| 3 |
������������Ҫ�������ô���ϵ������һ�κ����Ͷ��κ����Ľ���ʽ�����ɶ�����ƽ���ı��ε����ʣ����κ���ͼ���ϵ������������֪ʶ�㣬�����Ĺؼ����ۺ�������Щ֪ʶ���м��㣮�����ۺ���ǿ����һ���ѶȽϴ����Ŀ��

��ϰ��ϵ�д�
�����Ŀ
 ���ڵ�A������A�ֱ���x�ᡢy��Ĵ��ߣ�����Ϊ��B��C������ı���OBAC�������Σ���һ�κ����Ĺ�ϵʽ��
���ڵ�A������A�ֱ���x�ᡢy��Ĵ��ߣ�����Ϊ��B��C������ı���OBAC�������Σ���һ�κ����Ĺ�ϵʽ�� 5����ͼ��ʾ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ��-2��0���ͣ�2��0�����������Ƶ�B˳ʱ����ת90��õ������ڣ����A�Ķ�Ӧ��A�������Ϊ��������
5����ͼ��ʾ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ��-2��0���ͣ�2��0�����������Ƶ�B˳ʱ����ת90��õ������ڣ����A�Ķ�Ӧ��A�������Ϊ�������� ��ͼ��ʾ����ƽ��ֱ������ϵ�У�һ�����Ӵӵ�P����ʼ���ι��ڵ�A��B��C��ѭ���Գ�����������һ�δӵ�P�������ڵ�A�ĶԳƵ�M�����ڶ��δӵ�M�������ڵ�B�ĶԳƵ�N���������δӵ�N�������ڵ�C�ĶԳƵ㴦���������ȥ��
��ͼ��ʾ����ƽ��ֱ������ϵ�У�һ�����Ӵӵ�P����ʼ���ι��ڵ�A��B��C��ѭ���Գ�����������һ�δӵ�P�������ڵ�A�ĶԳƵ�M�����ڶ��δӵ�M�������ڵ�B�ĶԳƵ�N���������δӵ�N�������ڵ�C�ĶԳƵ㴦���������ȥ�� ��ͼ��ʾ����ƽ��ֱ������ϵxoy�У���һ��Խ��߳��ֱ�Ϊ1��2��3��������A1B1C1O��A2B2C2B1��A3B3C3B2����Խ���OB1��B1B2��B2 B3���η�����y���ϣ����ڶ����غϣ������������з�ʽ���Խ��߳�Ϊn�ĵ�n�������εĶ���An������Ϊ
��ͼ��ʾ����ƽ��ֱ������ϵxoy�У���һ��Խ��߳��ֱ�Ϊ1��2��3��������A1B1C1O��A2B2C2B1��A3B3C3B2����Խ���OB1��B1B2��B2 B3���η�����y���ϣ����ڶ����غϣ������������з�ʽ���Խ��߳�Ϊn�ĵ�n�������εĶ���An������Ϊ BE��
BE��