题目内容
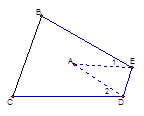
【题目】如图, 已知点A的坐标为(m,0)点B的坐标为(![]() ,0),在x轴上方取点C,使CB⊥x轴,且CB=2AO,点C,
,0),在x轴上方取点C,使CB⊥x轴,且CB=2AO,点C, ![]() 关于直线
关于直线![]() 对称,
对称, ![]() 交直线
交直线![]() 于点E若△BOE的面积为4,则点E的坐标为_______.
于点E若△BOE的面积为4,则点E的坐标为_______.
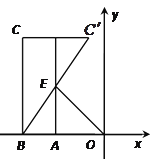
【答案】(4,4)或![]()
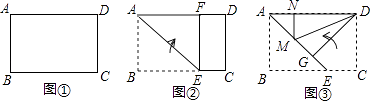
【解析】先根据矩形的性质与轴对称的性质得出AB=C′D,再利用AAS证明△ABE≌△DC′E,得出AE=DE=﹣m.根据△BOE的面积为4,列出方程(2﹣m)(﹣m)=4,解方程即可.
如图,设AE与CC′交于点D.
∵点A的坐标为(m,0),在x轴上方取点C,使CB⊥x轴,且CB=2AO, ∴CB=﹣2m.
∵点C,C′关于直线x=m对称,
∴CD=C′D,
∵ABCD是矩形,AB=CD,
∴AB=C′D.
又∵∠BAE=∠C′DE=90°,∠AEB=DEC′,
∴△ABE≌△DC′E,
∴AE=DE,
∴AE=AD=BC=﹣m.
∵△BOE的面积为4,
∴(2﹣m)(﹣m)=4,
整理得,m2﹣2m﹣8=0,
解得m=4或﹣2,
∵在x轴上方取点C,
∴﹣2m>0,
∴m<0,
∴m=4不合题意舍去,
“点睛”本题考查了矩形的性质,轴对称的性质,全等三角形的与性质,三角形的面积,得出AE=DE=﹣m是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目