题目内容
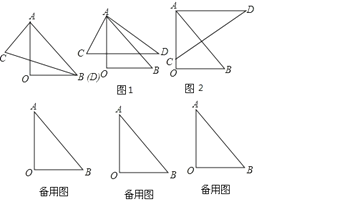
【题目】如图,矩形ABCD的边BC在x轴上,点A(a,4)和D分别在反比函数y=-![]() 和y=
和y=![]() (m>0)的图象上.
(m>0)的图象上.

(1)当AB=BC时,求m的值。
(2)连结OA,OD.当OD平方∠AOC时,求△AOD的周长.

【答案】(1)4 (2)10+2![]()
【解析】
(1)把A点坐标代入反比例函数式![]() ,求出a值,则A的横坐标可知,由条件知AB=BC,求出OC的长度,则求出D点的坐标,把D点坐标代入
,求出a值,则A的横坐标可知,由条件知AB=BC,求出OC的长度,则求出D点的坐标,把D点坐标代入![]() ,则可求出m的值.
,则可求出m的值.
(2)现知A点坐标,则可求出OA的长度,根据角平分线的定义和两直线平行内错角相等,等量代换得出 ∠ADO=∠AOD ,所以AO=AD=5,则OC的长度可求,现知DC的长度,用勾股定理即可求出OD的长度,则△AOD的周长可求.
(1)当y=4时,a=![]() =-3,
=-3,
∴OB=3.
∵矩形ABCD,且AB=BC,
∴AB=BC=CD=4,
∴OC=1,
∴D(1,4),
∴m=4.
(2)∵ ∠ABO=90°,A(-3,4),
∴OA=5.
∵OD平分∠AOC,
∴∠AOD=∠DOC.
∵AD∥BC,
∴∠ADO=∠DOC,
∴∠ADO=∠AOD,
∴DA=OA=5,
∴OC=2.
∵∠OCD=90°,
∴OD![]() ,
,
∴△AOD的周长是10+2![]() .
.

练习册系列答案
相关题目