��Ŀ����
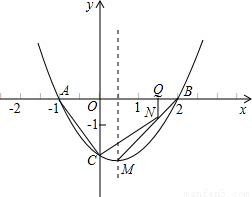
 ��֪���κ�����ͼ����ͼ��ʾ��
��֪���κ�����ͼ����ͼ��ʾ����1������κ����Ľ���ʽ�������߶���M�����ꣻ
��2������NΪ�߶�BM�ϵ�һ�㣬����N��x��Ĵ��ߣ�����Ϊ��Q������N���߶�BM���˶�ʱ����N�����B����M�غϣ�����NQ�ij�Ϊt���ı���NQAC�����Ϊs����s��t֮��ĺ�����ϵʽ���Ա���t��ȡֵ��Χ��
��3���ڶԳ����Ҳ�����������Ƿ���ڵ�P��ʹ��PACΪֱ�������Σ������ڣ�������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
��4������OAC���ɾ��Σ�ʹ�ϡ�OAC�����������Ϊ����һ�ߵ��������㣬�������������ھ�����һ�ߵĶԱ��ϣ���ֱ��д�����ε�δ֪�Ķ������꣨����Ҫ������̣���
���𰸡���������1�����ý���ʽ����������κ�������ʽ�������ù�ʽ������������꣬
��2�������������ֱ��BM����ʽ���ٱ�ʾ���ı��������
��3������ʹ��PACΪֱ�������Σ����������η���������ֱ��ʱ���ó���ͬ���ۣ�
��4���������Σ����ù��ɶ������������
��� �⣺��1���������ߵĽ���ʽy=a��x+1����x-2����
�⣺��1���������ߵĽ���ʽy=a��x+1����x-2����
��-2=a×1×��-2����
��a=1��
��y=x2-x-2���䶥�������ǣ� ��-
��- ����
����
��2�����߶�BM���ڵ�ֱ�ߵĽ���ʽΪ��y=kx+b����N������ΪN��h��-t����
�� ��
��
��������ɵķ�����ã� ��
��
�����߶�BM���ڵ�ֱ�ߵĽ���ʽΪ��y= x-3��
x-3��
N����������-t��
��-t= h-3��
h-3��
��h=2- t��
t��
���� ��h��2��
��h��2��
��s= ��2+t����2-
��2+t����2- t��=-
t��=- t2+
t2+ t+3��
t+3��
��s��t��ĺ�������ʽΪ��
s=- t2+
t2+ t+3��
t+3��
��M�������ǣ� ��-
��- ����
����
��QN���ֵΪ�� ��
��
���Ա�����ȡֵΧ�ǣ� ��
��
��3�����ڷ��������ĵ�P���������ǣ�P1�� ��
�� ����P2��
����P2�� ����
����
���P������ΪP��m��n������ n=m2-m-2��PA2=��m+1��2+n2
PC2=m2+��n+2��2��AC2=5��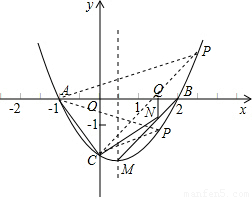
�����¼���������ۣ�
����������APC=90°��AC2=PC2+AP2��
�ɵã�m2+��n+2��2+��m+1��2+n2=5��
��ã� ��m2=-1����ȥ����
��m2=-1����ȥ����
���Ե�P�� ��
�� ��
��
����������PAC=90°����PC2=PA2+AC2
��n=m2-m-2
��m+1��2+n2=m2+��n+2��2+5
��ã�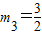 ��m4=0����ȥ�������Ե�P��
��m4=0����ȥ�������Ե�P�� ��-
��- ����
����
��������ͼ��۲�ã�����P�ڶԳ����Ҳ�ʱ��PA��AC�����Ա�AC�ĶԽǡ�APC��������ֱ�ǣ�
��4���Ե�O����A�����O����C��Ϊ���ε��������㣬�������������ھ�����һ��OA�����OC���ĶԱ��ϣ�
��ͼ����ʱδ֪���������ǵ�P��-1��-2�����Ե�A����CΪ���ε������㣬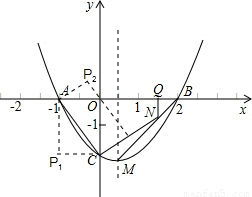
�������������ھ�����һ��AC�ĶԱ��ϣ�
��ͼ����ʱδ֪����������P1��-1��-2����P2��- ����
����
�� ��-
��- ����
����
������������Ҫ�����˶��κ�������ʽ�����Լ�����������㣬�ı���������㣬���ε����ʵȣ��ۺ��ԱȽ�ǿ��
��2�������������ֱ��BM����ʽ���ٱ�ʾ���ı��������
��3������ʹ��PACΪֱ�������Σ����������η���������ֱ��ʱ���ó���ͬ���ۣ�
��4���������Σ����ù��ɶ������������
���
 �⣺��1���������ߵĽ���ʽy=a��x+1����x-2����
�⣺��1���������ߵĽ���ʽy=a��x+1����x-2������-2=a×1×��-2����
��a=1��
��y=x2-x-2���䶥�������ǣ�
 ��-
��- ����
������2�����߶�BM���ڵ�ֱ�ߵĽ���ʽΪ��y=kx+b����N������ΪN��h��-t����
��
 ��
����������ɵķ�����ã�
 ��
�������߶�BM���ڵ�ֱ�ߵĽ���ʽΪ��y=
 x-3��
x-3��N����������-t��
��-t=
 h-3��
h-3����h=2-
 t��
t������
 ��h��2��
��h��2����s=
 ��2+t����2-
��2+t����2- t��=-
t��=- t2+
t2+ t+3��
t+3����s��t��ĺ�������ʽΪ��
s=-
 t2+
t2+ t+3��
t+3����M�������ǣ�
 ��-
��- ����
������QN���ֵΪ��
 ��
�����Ա�����ȡֵΧ�ǣ�
 ��
����3�����ڷ��������ĵ�P���������ǣ�P1��
 ��
�� ����P2��
����P2��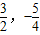 ����
�������P������ΪP��m��n������ n=m2-m-2��PA2=��m+1��2+n2
PC2=m2+��n+2��2��AC2=5��

�����¼���������ۣ�
����������APC=90°��AC2=PC2+AP2��
�ɵã�m2+��n+2��2+��m+1��2+n2=5��
��ã�
 ��m2=-1����ȥ����
��m2=-1����ȥ�������Ե�P��
 ��
�� ��
������������PAC=90°����PC2=PA2+AC2
��n=m2-m-2
��m+1��2+n2=m2+��n+2��2+5
��ã�
 ��m4=0����ȥ�������Ե�P��
��m4=0����ȥ�������Ե�P�� ��-
��- ����
������������ͼ��۲�ã�����P�ڶԳ����Ҳ�ʱ��PA��AC�����Ա�AC�ĶԽǡ�APC��������ֱ�ǣ�
��4���Ե�O����A�����O����C��Ϊ���ε��������㣬�������������ھ�����һ��OA�����OC���ĶԱ��ϣ�
��ͼ����ʱδ֪���������ǵ�P��-1��-2�����Ե�A����CΪ���ε������㣬

�������������ھ�����һ��AC�ĶԱ��ϣ�
��ͼ����ʱδ֪����������P1��-1��-2����P2��-
 ����
������
 ��-
��- ����
����������������Ҫ�����˶��κ�������ʽ�����Լ�����������㣬�ı���������㣬���ε����ʵȣ��ۺ��ԱȽ�ǿ��

��ϰ��ϵ�д�
 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д�
�����Ŀ
 ��֪���κ�����ͼ������ͼ�������н����У���ȷ�Ľ����У�������
��֪���κ�����ͼ������ͼ�������н����У���ȷ�Ľ����У���������a+b+c��0 ��a-b+c��0 ��abc��0 ��b=2a ��b��0��
| A��5�� | B��4�� | C��3�� | D��2�� |
 14����֪���κ�����ͼ����ͼ��ʾ����ô�˺����Ľ���ʽ�����ǣ�������
14����֪���κ�����ͼ����ͼ��ʾ����ô�˺����Ľ���ʽ�����ǣ�������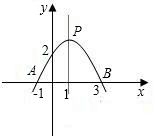 ��֪���κ�����ͼ����ͼ��ʾ������ͼ�е����ݣ�
��֪���κ�����ͼ����ͼ��ʾ������ͼ�е����ݣ� 21����֪���κ�����ͼ����ͼ��ʾ�������Ľ���ʽ��
21����֪���κ�����ͼ����ͼ��ʾ�������Ľ���ʽ�� ��֪���κ�����ͼ����ͼ��ʾ��
��֪���κ�����ͼ����ͼ��ʾ��