题目内容
 已知二次函数的图象如图所示,
已知二次函数的图象如图所示,(1)求二次函数的解析式及顶点M的坐标;
(2)若点N为线段BM上的一点,过点N作NQ⊥X轴于点Q,当点N在BM上运动时(点N不与点B、点M重合),设NQ的长为t,四边形NQAC的面积
没有空
没有空
为S,求S与t之间的函数关系式及自变量的取值范围;(3)在对称轴右侧的抛物线上是否存在点P,使△PAC为直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
分析:(1)根据A与B的横坐标,设出抛物线的二根式方程,将C坐标代入求出a的值,确定出抛物线解析式,将解析式化为顶点坐标式,即可求出抛物线顶点M的坐标.
(2)根据抛物线的解析式可求出A、B、C三点的坐标,进而可求出直线BM的解析式,已知了QN=t,即N点纵坐标为-t,代入直线BM的解析式中,可求得Q点的横坐标即OQ得长,分别求出△OAC、梯形QNCO的面积,它们的面积和即为所求的四边形QNCO的面积,由此可求出S、t的函数关系式.
(3)根据函数的图象及A、C的位置,可明显的看出∠APC不可能是直角,因此此题要分两种情况讨论:
①∠PAC=90°,设出点P的坐标,然后表示出AC2、PA2、PC2的值,根据勾股定理可得到关于P点横、纵坐标的等量关系式,联立抛物线的解析式,即可求出此时点P的坐标;
②∠PCA=90°,解法同①.
(2)根据抛物线的解析式可求出A、B、C三点的坐标,进而可求出直线BM的解析式,已知了QN=t,即N点纵坐标为-t,代入直线BM的解析式中,可求得Q点的横坐标即OQ得长,分别求出△OAC、梯形QNCO的面积,它们的面积和即为所求的四边形QNCO的面积,由此可求出S、t的函数关系式.
(3)根据函数的图象及A、C的位置,可明显的看出∠APC不可能是直角,因此此题要分两种情况讨论:
①∠PAC=90°,设出点P的坐标,然后表示出AC2、PA2、PC2的值,根据勾股定理可得到关于P点横、纵坐标的等量关系式,联立抛物线的解析式,即可求出此时点P的坐标;
②∠PCA=90°,解法同①.
解答: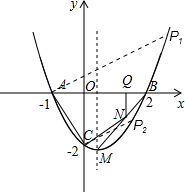 解:(1)设抛物线解析式为y=a(x+1)(x-2),
解:(1)设抛物线解析式为y=a(x+1)(x-2),
将x=0,y=-2代入得:a=1,
∴抛物线y=x2-x-2=(x-
)2-
,
∴顶点M的坐标为(
,-
);
(2)抛物线与y=x2-x-2与x轴的两交点为A(-1,0),B(2,0),
设线段BM所在直线的解析式为y=kx+b,
则
,
解得
;
故线段BM所在直线的解析式为y=
x-3,
设点N的坐标为(x,-t),
∵点N在线段BM上,
∴-t=
x-3,
∴x=-
t+2,
∴S四边形NQAC=S△AOC+S梯形OQNC=
×1×2+
×(2+t)×(-
t+2)=-
t2+
t+3,
∴S与t之间的函数关系式为S=-
t2+
t+3,自变量t的取值范围为0<t<
;
(3)假设存在符合条件的点P,设点P的坐标为P(m,n),则m>
且n=m2-m-2;
PA2=(m+1)2+n2,PC2=m2+(n+2)2,AC2=5,
分以下几种情况讨论:
①若∠PAC=90°,则PC2=PA2+AC2.
∴
,
解得:m1=
,m2=-1;
∵m>
,∴m=
,
∴P1(
,
);
②若∠PCA=90°,则PA2=PC2+AC2,
则
,
解得:m3=
,m4=0,
∵m>
,
∴m=
,
∴P2(
,-
),
当点P在对称轴右侧时,PA>AC,
∴边AC的对角∠APC不可能是直角,
∴存在符合条件的点P,坐标分别为P1(
,
);P2(
,-
).
 解:(1)设抛物线解析式为y=a(x+1)(x-2),
解:(1)设抛物线解析式为y=a(x+1)(x-2),将x=0,y=-2代入得:a=1,
∴抛物线y=x2-x-2=(x-
| 1 |
| 2 |
| 9 |
| 4 |
∴顶点M的坐标为(
| 1 |
| 2 |
| 9 |
| 4 |
(2)抛物线与y=x2-x-2与x轴的两交点为A(-1,0),B(2,0),
设线段BM所在直线的解析式为y=kx+b,
则
|
解得
|
故线段BM所在直线的解析式为y=
| 3 |
| 2 |
设点N的坐标为(x,-t),
∵点N在线段BM上,
∴-t=
| 2 |
| 3 |
∴x=-
| 3 |
| 2 |
∴S四边形NQAC=S△AOC+S梯形OQNC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴S与t之间的函数关系式为S=-
| 1 |
| 3 |
| 1 |
| 3 |
| 9 |
| 4 |
(3)假设存在符合条件的点P,设点P的坐标为P(m,n),则m>
| 1 |
| 2 |
PA2=(m+1)2+n2,PC2=m2+(n+2)2,AC2=5,
分以下几种情况讨论:
①若∠PAC=90°,则PC2=PA2+AC2.
∴
|
解得:m1=
| 5 |
| 2 |
∵m>
| 1 |
| 2 |
| 5 |
| 2 |
∴P1(
| 5 |
| 2 |
| 7 |
| 4 |
②若∠PCA=90°,则PA2=PC2+AC2,
则
|
解得:m3=
| 3 |
| 2 |
∵m>
| 1 |
| 2 |
∴m=
| 3 |
| 2 |
∴P2(
| 3 |
| 2 |
| 5 |
| 4 |
当点P在对称轴右侧时,PA>AC,
∴边AC的对角∠APC不可能是直角,
∴存在符合条件的点P,坐标分别为P1(
| 5 |
| 2 |
| 7 |
| 4 |
| 3 |
| 2 |
| 5 |
| 4 |
点评:此题考查了二次函数综合题,涉及的知识有:坐标与图形性质,待定系数法求二次函数解析式,二次函数的图象与性质,利用了分类讨论的思想,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 已知二次函数的图象如右图,则下列结论中,正确的结论有( )
已知二次函数的图象如右图,则下列结论中,正确的结论有( )①a+b+c>0 ②a-b+c<0 ③abc<0 ④b=2a ⑤b>0.
| A、5个 | B、4个 | C、3个 | D、2个 |
 14、已知二次函数的图象如图所示,那么此函数的解析式可能是( )
14、已知二次函数的图象如图所示,那么此函数的解析式可能是( )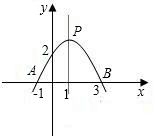 已知二次函数的图象如图所示,根据图中的数据,
已知二次函数的图象如图所示,根据图中的数据, 21、已知二次函数的图象如图所示,求它的解析式.
21、已知二次函数的图象如图所示,求它的解析式.