题目内容
【题目】如图,在等腰![]() 中,
中,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交过点
,交过点![]() 直线
直线![]() 交于点
交于点![]() ,且
,且![]() ,
,![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() 时,则
时,则![]() ________.
________.

【答案】![]()
【解析】
作辅助线构建等腰直角三角形和直角三角形,分别得出△BDF和△AFM是等腰直角三角形,得BF=DB=1,AM=FM,根据sin∠ABC=![]() 设未知数,表示BM和AM的长,列方程得出各线段的长,并证出AG是△EFC的中位线,由此得出结论.
设未知数,表示BM和AM的长,列方程得出各线段的长,并证出AG是△EFC的中位线,由此得出结论.
过A作AM⊥BC,垂足为M,延长AD、CB交于F,取FC的中点G,连接AG,
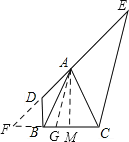
∵∠ADB=135°,
∴∠BDF=180°-135°=45°,
∴△BDF是等腰直角三角形,
∴BF=DB=1,
由勾股定理得:DF=![]() ,
,
在Rt△AFM中,∵∠F=45°,
∴AM=FM,
设AM=2![]() x,AB=5x,则BM=
x,AB=5x,则BM=![]() x,
x,
由AM=FM得:![]() x+1=2
x+1=2![]() x,
x,
x=![]() ,
,
∴BM=MC=![]() x=1,AM=2,
x=1,AM=2,
∵AM⊥BC,DB⊥BC,
∴DB∥AM,
∵FB=BM,
∴FD=AD,
∵AE=2AD,
∴AE=AF,
∴AG是△EFC的中位线,
∴EC=2AG,
∵MG=![]() ,
,
由勾股定理得:AG=![]() =
=![]() ,
,
∴EC=![]() .
.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
【题目】深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.
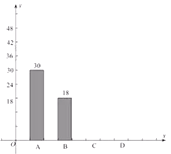
类型 | 频数 | 频率 |
A | 30 |
|
B | 18 | 0.15 |
C |
| 0.40 |
D |
|
|
(1)学生共________人, ![]() ________,
________, ![]() ________;
________;
(2)补全条形统计图;
(3)若该校共有2000人,骑共享单车的有________人.