Question

【题目】如图，∠ACB＝90°，AC＝BC，AD⊥CE，BE⊥CE，垂足分别为点D，E．（1）求证：△ACD≌△CBE；（2）若BE=5，AD=12，求DE的长．

Answer 1

【答案】(1)见解析；（2）7.

【解析】

（1）由题意可得∠BCE＝∠A，且∠E＝∠CDA＝90°，AC＝BC，即可得出结论；

（2）由△ACD≌△CBE，可得CE＝AD＝12，BE＝CD＝5，即可得出结果．

（1）证明：∵AD⊥CE，BE⊥CE，

∴∠ADC＝∠E＝90°

∴∠A+∠DCA＝90°，

∵∠ACB＝∠DCA+∠BCE＝90°，

∴∠A＝∠BCE，

在△ACD和△CBE中，

，

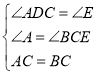∴△ACD≌△CBE（AAS）；

（2）由（1）得：△ACD≌△CBE，

∴CE＝AD＝12，BE＝CD＝5，

∴DE＝CE﹣CD＝12﹣5＝7．