题目内容
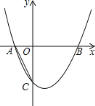
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,点
两点,点![]() 在
在![]() 轴的负半轴,点
轴的负半轴,点![]() 在
在![]() 轴的正半轴,与
轴的正半轴,与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,
,![]() ,
,![]() .则下列判断中正确的是( )
.则下列判断中正确的是( )
A. 此抛物线的解析式为![]()
B. 当![]() 时,
时,![]() 随着
随着![]() 的增大而增大
的增大而增大
C. 此抛物线与直线![]() 只有一个交点
只有一个交点
D. 在此抛物线上的某点![]() ,使
,使![]() 的面积等于
的面积等于![]() ,这样的点共有三个
,这样的点共有三个
【答案】C
【解析】
利用CO=2AO,而CO=BO,AB=3,可得出AO=1,BO=OC=2,即可求出二次函数的解析式,由二次函数的对称轴,可得出当x>0时,y随着x的增大而先减小再增大,由二次函数的最小值为-![]() ,可得此抛物线与直线y=-
,可得此抛物线与直线y=-![]() 只有一个交点,由△MAB的面积等于4,得出M到x轴的距离为
只有一个交点,由△MAB的面积等于4,得出M到x轴的距离为![]() ,这样的点共有2个.即可选出答案.
,这样的点共有2个.即可选出答案.
解:∵CO=2AO,而CO=BO,AB=3,
∴AO=1,BO=OC=2,即A(-1,0),B(2,0),C(0,-2),
∴二次函数的解析式为y=x2-x-2,故A错误.
∵二次函数的对称轴为x=![]() ,
,
∴当x>0时,y随着x的增大而先减小再增大,故B错误.
∵此二次函数的最小值为-![]() ,
,
∴此抛物线与直线y=-![]() 只有一个交点,C正确.
只有一个交点,C正确.
∵要使△MAB的面积等于4,须使M到x轴的距离为![]() ,这样的点共有2个,故B错误.
,这样的点共有2个,故B错误.
故选:C.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目