题目内容
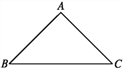
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=40°,以直角顶点C为旋转中心,将△ABC逆时针旋转到△A′B′C的位置,其中A′、B′分别是A、B的对应点,且点B在斜边A′B′上,直角边CA′交AB于D,则旋转角∠A CA′的度数为 .
【答案】80°
【解析】解:∵△ABC以点C为中心旋转到△A′B′C的位置,
∴∠B′=∠ABC,BC=B′C′,
∴∠CBB′=∠B′,
∵∠A=40°,
∴∠B′=∠ABC=90°﹣40°=50°,
∴∠BCB′=180°﹣2×50°=80°,
∵∠B′CB+∠BCA′=∠ACA′+∠BCA′,
∴∠B′CB=∠ACA′
∴∠ACA′=80°.
所以答案是:80°.
【考点精析】关于本题考查的旋转的性质,需要了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能得出正确答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目