题目内容
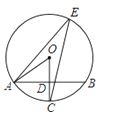
【题目】如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF.
(1)若CD=2![]() , AF=3,求⊙O的周长;
, AF=3,求⊙O的周长;
(2)求证:直线BE是⊙O的切线.
【答案】解:(1)连接OC.设半径为r,
∵OA⊥CD,
∴DF=FC=![]() ,
,
在RT△OFC中,∵∠OFC=90°,FC=![]() ,OF=r﹣3,OC=r,
,OF=r﹣3,OC=r,
∴r2=(r﹣3)2+(![]() )2 ,
)2 ,
∴r=4,
∴⊙O的周长为8π.
(2)证明:∵OA⊥CD,
∴DF=FC,AD=AC,∠AFD=90°
∴∠ADC=∠ACD,
∵∠E=∠ACD,
∴∠ADC=∠E,
∴CD∥EB,
∴∠AFD=∠ABE=90°,
∴BE是⊙O的切线.
【解析】(1)连接OC.设半径为r,在RT△OFC中利用勾股定理即可解决问题.
(2)只要证明CD∥EB,即可得到∠AFD=∠ABE=90°,由此可以得出结论.
【考点精析】根据题目的已知条件,利用切线的判定定理的相关知识可以得到问题的答案,需要掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目