题目内容
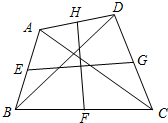
如图(l),在正方形ABCD中,点E、F分别在AB、BC上,且AE=BF,AF与DE交于点G.

(1)试探索线段AF、DE的数量和位置关系,写出你的结论并说明理由;
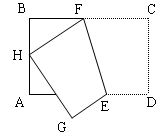
(2)连结EF、DF,分别取AE、EF、FD、DA的中点H、I、J、K,则四边形HIJK是什么特殊平行四边形?请在图(2)中补全图形,并说明理由.

(1)试探索线段AF、DE的数量和位置关系,写出你的结论并说明理由;
(2)连结EF、DF,分别取AE、EF、FD、DA的中点H、I、J、K,则四边形HIJK是什么特殊平行四边形?请在图(2)中补全图形,并说明理由.
(1) AF=DE且AF⊥DE,理由见解析(2)正方形,理由见解析
(1) AF=DE且AF⊥DE
在△ABF和△DAE中,
∵AB="DA," ∠B=∠DAE,BF=AE
∴△ABF≌△DAE
∴AF=DE, …………2分
∠BAF=∠ADE
又∵∠BAF+∠DAG=90o
∴∠ADE+∠DAG=90o
∴∠AGD=90o , 即AF⊥DE. …………4分
(2) 四边形HIJK是正方形
∵H、I、J、K分别是AE、EF、FD、DA的中点
∴HK∥DE且HK = ,IJ∥DE且IJ =
,IJ∥DE且IJ =
∴HK ∥IJ且HK =IJ
∴HIJK是平行四边形 …………6分
同理可证HI∥KJ且HI=KJ= ,
,
又∵AF=DE ∴HI=IJ ∴HIJK是菱形 …………8分
又∵AF⊥DE ∴HI⊥IJ
∴四边形HIJK是正方形. …………9分
(1)根据已知利用SAS判定△DAE≌△ABF,由全等三角形的判定方法可得到AF=DE.
(2)根据已知可得HK,KJ,IJ,HI都是中位线,由全等三角形的判定可得到四边形四边都相等且有一个角是直角,从而来可得到该四边形是正方形.
在△ABF和△DAE中,
∵AB="DA," ∠B=∠DAE,BF=AE
∴△ABF≌△DAE
∴AF=DE, …………2分
∠BAF=∠ADE
又∵∠BAF+∠DAG=90o
∴∠ADE+∠DAG=90o
∴∠AGD=90o , 即AF⊥DE. …………4分
(2) 四边形HIJK是正方形

∵H、I、J、K分别是AE、EF、FD、DA的中点
∴HK∥DE且HK =
 ,IJ∥DE且IJ =
,IJ∥DE且IJ =
∴HK ∥IJ且HK =IJ
∴HIJK是平行四边形 …………6分
同理可证HI∥KJ且HI=KJ=
 ,
, 又∵AF=DE ∴HI=IJ ∴HIJK是菱形 …………8分
又∵AF⊥DE ∴HI⊥IJ
∴四边形HIJK是正方形. …………9分
(1)根据已知利用SAS判定△DAE≌△ABF,由全等三角形的判定方法可得到AF=DE.
(2)根据已知可得HK,KJ,IJ,HI都是中位线,由全等三角形的判定可得到四边形四边都相等且有一个角是直角,从而来可得到该四边形是正方形.

练习册系列答案
相关题目



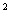 ,高为2cm,则此梯形的中位线长为 cm
,高为2cm,则此梯形的中位线长为 cm