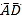Question

【题目】知识再现：

如果，，则线段的中点坐标为；对于两个一次函数和，若两个一次函数图象平行，则且；若两个一次函数图象垂直，则．

提醒：在下面这个相关问题中如果需要，你可以直接利用以上知识．

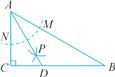
在平面直角坐标系中，已知点，．

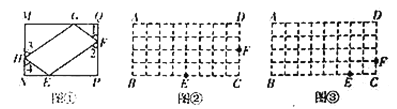
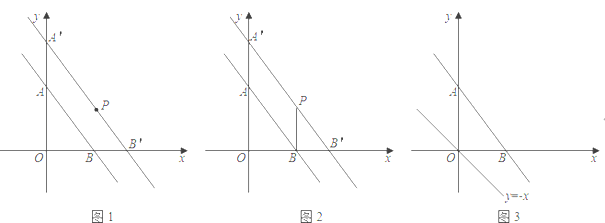
（1）如图1，把直线向右平移使它经过点，如果平移后的直线交轴于点，交x轴于点，请确定直线的解析式．

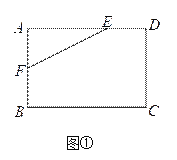
（2）如图2，连接，求的长．

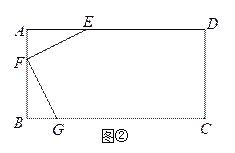
（3）已知点是直线上一个动点，以为对角线的四边形是平行四边形，当取最小值时，请在图3中画出满足条件的，并直接写出此时点坐标．

Answer 1

【答案】（1）；（2）5；（3）

【解析】

（1）用待定系数法可求直线AB的解析式，由平移的性质可设直线A'B'的解析式为：，将点P坐标代入可求直线A′B′的解析式；
（2）由P（6，4），B（6，0），点B'坐标（9，0）可得BP⊥B'B，BP=4，BB'=3，由勾股定理可求B'P的长；
（3）由平行四边形的性质可得，AE=BE，当CE⊥CO时，CE的值最小，即CD的值最小，由中点坐标公式可求点E坐标，可求CE解析式，列出方程组可求点C坐标．

解：（1）设直线的解析式为：，过点两点，有

∴，∴

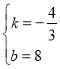
直线的解析式为： ，

把直线向右平移使它经过点

∴直线的解析式为，且过点

∴，∴

∴直线的解析式为

（2）∵直线交轴于点，交轴于点

∴当时，

当时，

∴点坐标，点坐标

∵，，点坐标

∴轴，，，

∴

（3）如图，设与的交点为，

∵四边形是平行四边形，

∴，，

∴要使取最小值，即的值最小，

由垂线段最短可得：当时，的值最小，即的值最小，

∵点，，且

∴点

∵，直线解析式为：

∴设解析式为，且过点

∴

∴

∴解析式为

∴联立直线和的解析式成方程组，得

解得：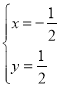

∴点